Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 101888 by bemath last updated on 05/Jul/20

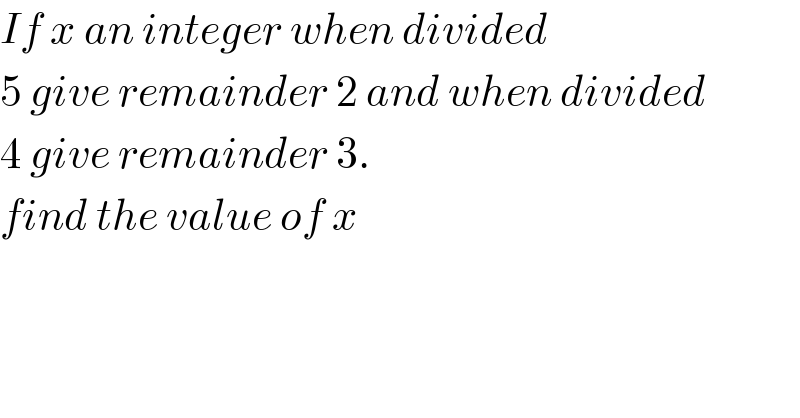
If x an integer when divided 5 give remainder 2 and when divided 4 give remainder 3. find the value of x

$${If}\:{x}\:{an}\:{integer}\:{when}\:{divided} \\ $$$$\mathrm{5}\:{give}\:{remainder}\:\mathrm{2}\:{and}\:{when}\:{divided} \\ $$$$\mathrm{4}\:{give}\:{remainder}\:\mathrm{3}. \\ $$$${find}\:{the}\:{value}\:{of}\:{x} \\ $$

Commented by Rasheed.Sindhi last updated on 05/Jul/20

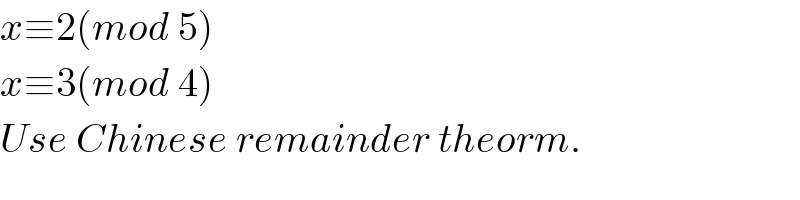
x≡2(mod 5) x≡3(mod 4) Use Chinese remainder theorm.

$${x}\equiv\mathrm{2}\left({mod}\:\mathrm{5}\right) \\ $$$${x}\equiv\mathrm{3}\left({mod}\:\mathrm{4}\right) \\ $$$${Use}\:{Chinese}\:{remainder}\:{theorm}. \\ $$

Answered by Rasheed.Sindhi last updated on 05/Jul/20

x−2 is divisible by 5 x=5m+2 x−3 is divisible by 4 x=4n+3 5m+2=4n+3 m=((4n+1)/5) ; m,n∈N n=1⇒m=1⇒x=7 n=6⇒m=5⇒x=27 n=11⇒m=9⇒x=47 ...... ....

$${x}−\mathrm{2}\:{is}\:{divisible}\:{by}\:\mathrm{5} \\ $$$${x}=\mathrm{5}{m}+\mathrm{2} \\ $$$${x}−\mathrm{3}\:{is}\:{divisible}\:{by}\:\mathrm{4} \\ $$$${x}=\mathrm{4}{n}+\mathrm{3} \\ $$$$\mathrm{5}{m}+\mathrm{2}=\mathrm{4}{n}+\mathrm{3} \\ $$$${m}=\frac{\mathrm{4}{n}+\mathrm{1}}{\mathrm{5}}\:;\:{m},{n}\in\mathbb{N} \\ $$$${n}=\mathrm{1}\Rightarrow{m}=\mathrm{1}\Rightarrow{x}=\mathrm{7} \\ $$$${n}=\mathrm{6}\Rightarrow{m}=\mathrm{5}\Rightarrow{x}=\mathrm{27} \\ $$$${n}=\mathrm{11}\Rightarrow{m}=\mathrm{9}\Rightarrow{x}=\mathrm{47} \\ $$$$...... \\ $$$$.... \\ $$

Answered by john santu last updated on 05/Jul/20

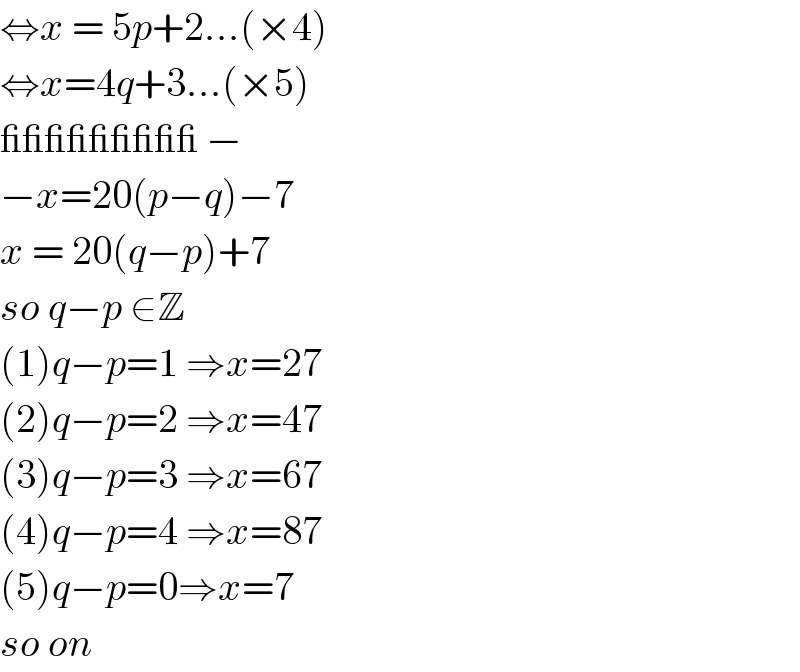
⇔x = 5p+2...(×4) ⇔x=4q+3...(×5) _________ − −x=20(p−q)−7 x = 20(q−p)+7 so q−p ∈Z (1)q−p=1 ⇒x=27 (2)q−p=2 ⇒x=47 (3)q−p=3 ⇒x=67 (4)q−p=4 ⇒x=87 (5)q−p=0⇒x=7 so on

$$\Leftrightarrow{x}\:=\:\mathrm{5}{p}+\mathrm{2}...\left(×\mathrm{4}\right) \\ $$$$\Leftrightarrow{x}=\mathrm{4}{q}+\mathrm{3}...\left(×\mathrm{5}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\:− \\ $$$$−{x}=\mathrm{20}\left({p}−{q}\right)−\mathrm{7} \\ $$$${x}\:=\:\mathrm{20}\left({q}−{p}\right)+\mathrm{7} \\ $$$${so}\:{q}−{p}\:\in\mathbb{Z} \\ $$$$\left(\mathrm{1}\right){q}−{p}=\mathrm{1}\:\Rightarrow{x}=\mathrm{27} \\ $$$$\left(\mathrm{2}\right){q}−{p}=\mathrm{2}\:\Rightarrow{x}=\mathrm{47} \\ $$$$\left(\mathrm{3}\right){q}−{p}=\mathrm{3}\:\Rightarrow{x}=\mathrm{67} \\ $$$$\left(\mathrm{4}\right){q}−{p}=\mathrm{4}\:\Rightarrow{x}=\mathrm{87}\: \\ $$$$\left(\mathrm{5}\right){q}−{p}=\mathrm{0}\Rightarrow{x}=\mathrm{7} \\ $$$${so}\:{on}\: \\ $$

Answered by mathmax by abdo last updated on 05/Jul/20

x≡2[5] and x ≡3 4] ⇒x =5n +2 and x =4m+3 ⇒ 5n+2 =4m+3 let use congruence modulo 5(prime) ⇒ 2^− =−m^− +3^− ⇒m^− = 3^− −2^− =1^− ⇒m =5q+1 ⇒x =4(5q+1)+3 ⇒x =20q +7

$$\left.\mathrm{x}\equiv\mathrm{2}\left[\mathrm{5}\right]\:\mathrm{and}\:\mathrm{x}\:\equiv\mathrm{3}\:\:\mathrm{4}\right]\:\Rightarrow\mathrm{x}\:=\mathrm{5n}\:+\mathrm{2}\:\mathrm{and}\:\mathrm{x}\:=\mathrm{4m}+\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{5n}+\mathrm{2}\:=\mathrm{4m}+\mathrm{3}\:\:\mathrm{let}\:\mathrm{use}\:\mathrm{congruence}\:\mathrm{modulo}\:\mathrm{5}\left(\mathrm{prime}\right)\:\Rightarrow \\ $$$$\overset{−} {\mathrm{2}}\:=−\overset{−} {\mathrm{m}}\:\:+\overset{−} {\mathrm{3}}\Rightarrow\overset{−} {\mathrm{m}}\:=\:\overset{−} {\mathrm{3}}−\overset{−} {\mathrm{2}}\:=\overset{−} {\mathrm{1}}\:\:\Rightarrow\mathrm{m}\:=\mathrm{5q}+\mathrm{1}\:\Rightarrow\mathrm{x}\:=\mathrm{4}\left(\mathrm{5q}+\mathrm{1}\right)+\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}\:=\mathrm{20q}\:+\mathrm{7} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com