
Question Number 202258 by MATHEMATICSAM last updated on 23/Dec/23
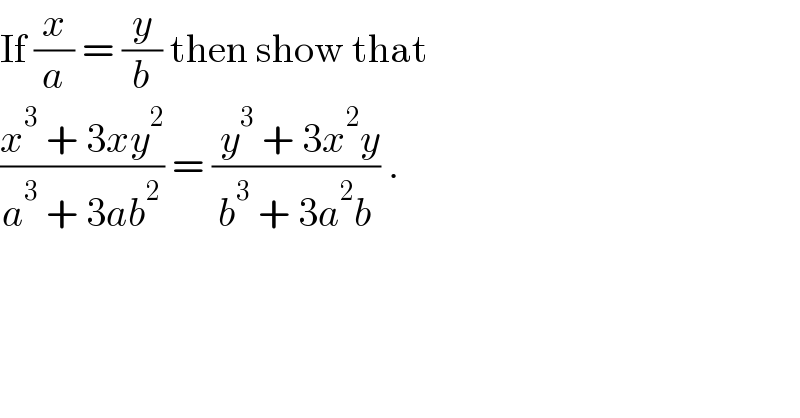
$$\mathrm{If}\:\frac{{x}}{{a}}\:=\:\frac{{y}}{{b}}\:\mathrm{then}\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\frac{{x}^{\mathrm{3}} \:+\:\mathrm{3}{xy}^{\mathrm{2}} }{{a}^{\mathrm{3}} \:+\:\mathrm{3}{ab}^{\mathrm{2}} }\:=\:\frac{\:{y}^{\mathrm{3}} \:+\:\mathrm{3}{x}^{\mathrm{2}} {y}}{{b}^{\mathrm{3}} \:+\:\mathrm{3}{a}^{\mathrm{2}} {b}}\:. \\ $$
Answered by deleteduser1 last updated on 23/Dec/23
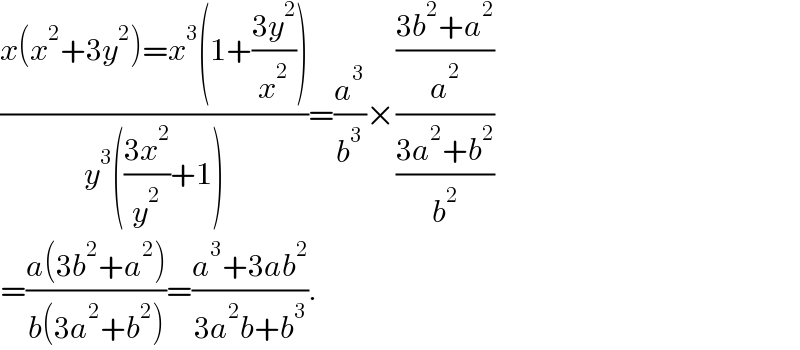
$$\frac{{x}\left({x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} \right)={x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{3}{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}{{y}^{\mathrm{3}} \left(\frac{\mathrm{3}{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }+\mathrm{1}\right)}=\frac{{a}^{\mathrm{3}} }{{b}^{\mathrm{3}} }×\frac{\frac{\mathrm{3}{b}^{\mathrm{2}} +{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{\frac{\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }} \\ $$$$=\frac{{a}\left(\mathrm{3}{b}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{{b}\left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}=\frac{{a}^{\mathrm{3}} +\mathrm{3}{ab}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} }. \\ $$
Answered by Rasheed.Sindhi last updated on 23/Dec/23
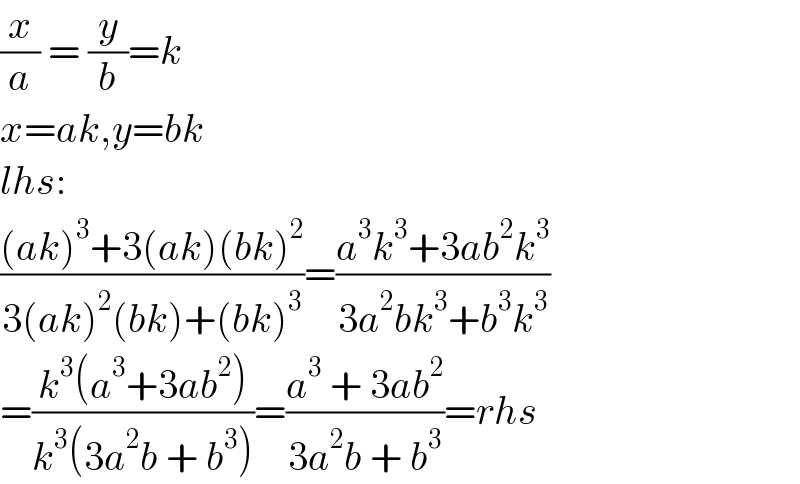
$$\frac{{x}}{{a}}\:=\:\frac{{y}}{{b}}={k} \\ $$$${x}={ak},{y}={bk} \\ $$$${lhs}: \\ $$$$\frac{\left({ak}\right)^{\mathrm{3}} +\mathrm{3}\left({ak}\right)\left({bk}\right)^{\mathrm{2}} }{\mathrm{3}\left({ak}\right)^{\mathrm{2}} \left({bk}\right)+\left({bk}\right)^{\mathrm{3}} }=\frac{{a}^{\mathrm{3}} {k}^{\mathrm{3}} +\mathrm{3}{ab}^{\mathrm{2}} {k}^{\mathrm{3}} }{\mathrm{3}{a}^{\mathrm{2}} {bk}^{\mathrm{3}} +{b}^{\mathrm{3}} {k}^{\mathrm{3}} } \\ $$$$=\frac{{k}^{\mathrm{3}} \left({a}^{\mathrm{3}} +\mathrm{3}{ab}^{\mathrm{2}} \right)}{{k}^{\mathrm{3}} \left(\mathrm{3}{a}^{\mathrm{2}} {b}\:+\:{b}^{\mathrm{3}} \right)}=\frac{{a}^{\mathrm{3}} \:+\:\mathrm{3}{ab}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} {b}\:+\:{b}^{\mathrm{3}} }={rhs} \\ $$
Answered by Frix last updated on 23/Dec/23
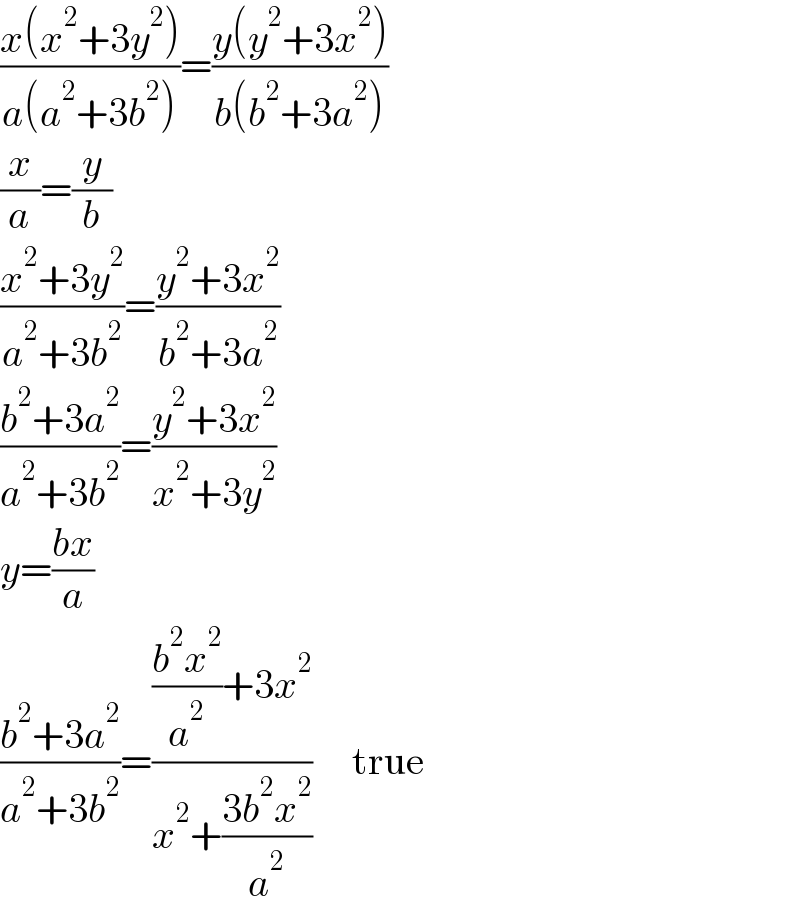
$$\frac{{x}\left({x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} \right)}{{a}\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)}=\frac{{y}\left({y}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} \right)}{{b}\left({b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)} \\ $$$$\frac{{x}}{{a}}=\frac{{y}}{{b}} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} } \\ $$$$\frac{{b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} } \\ $$$${y}=\frac{{bx}}{{a}} \\ $$$$\frac{{b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} }=\frac{\frac{{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\frac{\mathrm{3}{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:\:\:\:\:\mathrm{true} \\ $$
