
Question Number 217952 by dscm last updated on 23/Mar/25
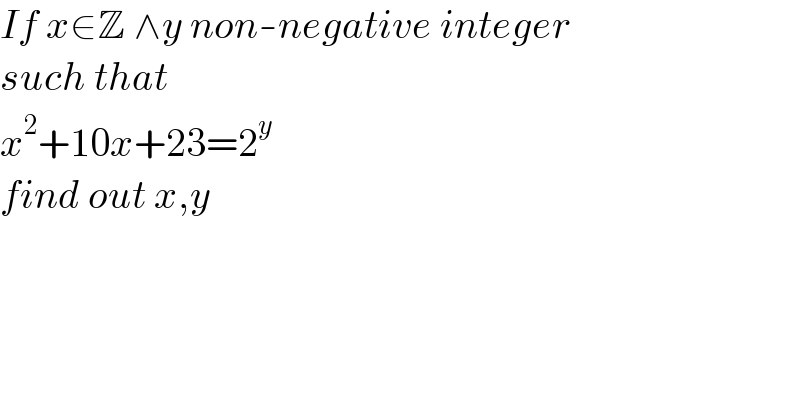
$${If}\:{x}\in\mathbb{Z}\:\wedge{y}\:{non}-{negative}\:{integer} \\ $$$${such}\:{that} \\ $$$${x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{23}=\mathrm{2}^{{y}} \\ $$$${find}\:{out}\:{x},{y} \\ $$
Answered by Frix last updated on 23/Mar/25
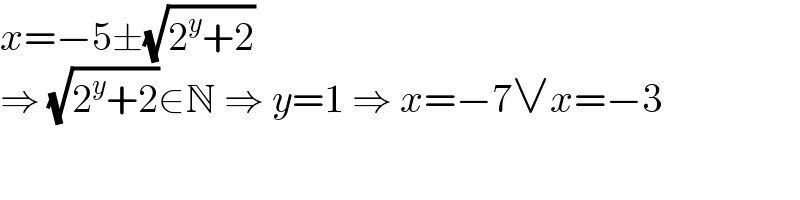
$${x}=−\mathrm{5}\pm\sqrt{\mathrm{2}^{{y}} +\mathrm{2}} \\ $$$$\Rightarrow\:\sqrt{\mathrm{2}^{{y}} +\mathrm{2}}\in\mathbb{N}\:\Rightarrow\:{y}=\mathrm{1}\:\Rightarrow\:{x}=−\mathrm{7}\vee{x}=−\mathrm{3} \\ $$
Commented by dscm last updated on 23/Mar/25
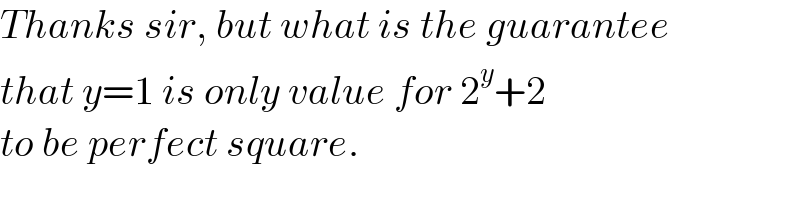
$${Thanks}\:{sir},\:{but}\:{what}\:{is}\:{the}\:{guarantee} \\ $$$${that}\:{y}=\mathrm{1}\:{is}\:{only}\:{value}\:{for}\:\mathrm{2}^{{y}} +\mathrm{2} \\ $$$${to}\:{be}\:{perfect}\:{square}. \\ $$
Answered by Ghisom last updated on 23/Mar/25
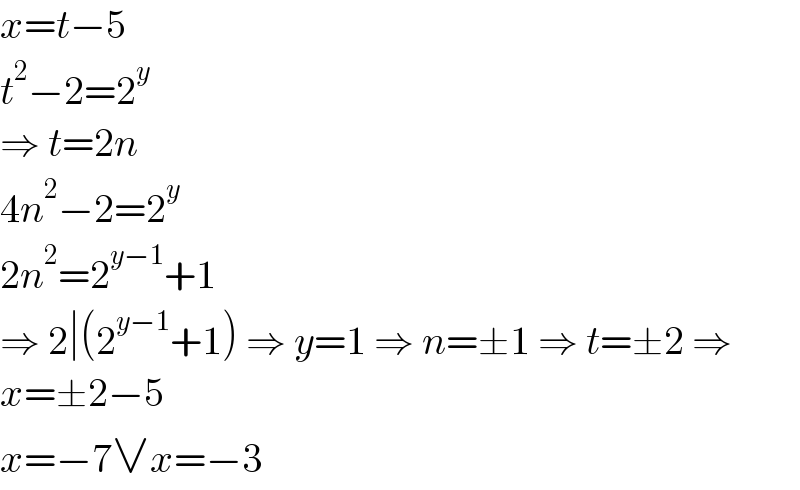
$${x}={t}−\mathrm{5} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}=\mathrm{2}^{{y}} \\ $$$$\Rightarrow\:{t}=\mathrm{2}{n} \\ $$$$\mathrm{4}{n}^{\mathrm{2}} −\mathrm{2}=\mathrm{2}^{{y}} \\ $$$$\mathrm{2}{n}^{\mathrm{2}} =\mathrm{2}^{{y}−\mathrm{1}} +\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{2}\mid\left(\mathrm{2}^{{y}−\mathrm{1}} +\mathrm{1}\right)\:\Rightarrow\:{y}=\mathrm{1}\:\Rightarrow\:{n}=\pm\mathrm{1}\:\Rightarrow\:{t}=\pm\mathrm{2}\:\Rightarrow \\ $$$${x}=\pm\mathrm{2}−\mathrm{5} \\ $$$${x}=−\mathrm{7}\vee{x}=−\mathrm{3} \\ $$
