Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 133981 by bemath last updated on 26/Feb/21

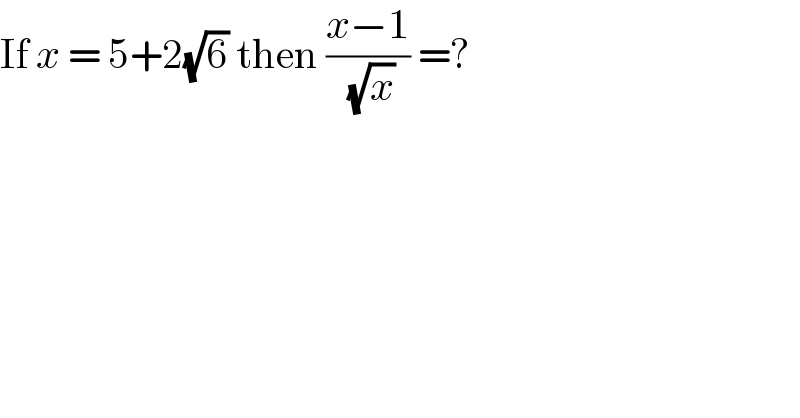
If x = 5+2(√6) then ((x−1)/( (√x))) =?

$$\mathrm{If}\:{x}\:=\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:\mathrm{then}\:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}}}\:=? \\ $$

Answered by Dwaipayan Shikari last updated on 26/Feb/21

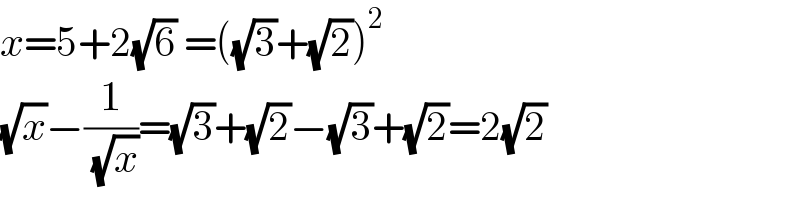
x=5+2(√6) =((√3)+(√2))^2 (√x)−(1/( (√x)))=(√3)+(√2)−(√3)+(√2)=2(√2)

$${x}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:=\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\sqrt{{x}}−\frac{\mathrm{1}}{\:\sqrt{{x}}}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$

Commented by malwan last updated on 26/Feb/21

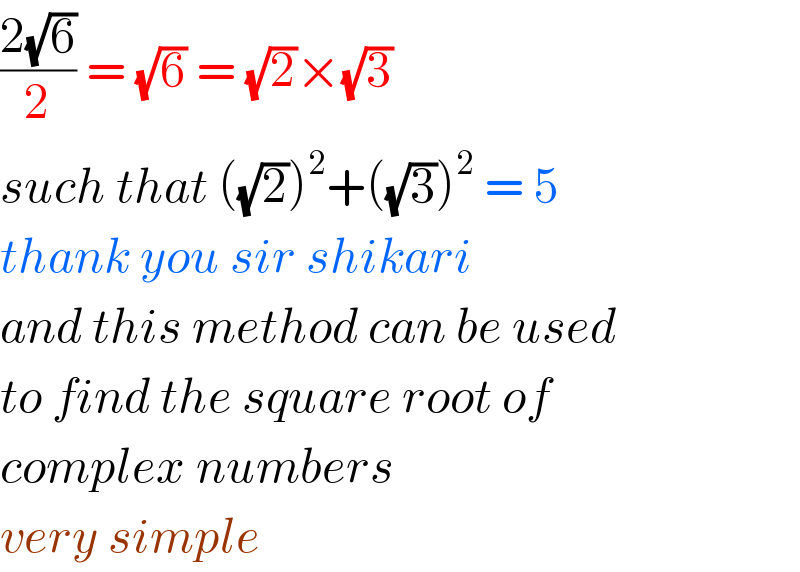
((2(√6))/2) = (√6) = (√2)×(√3) such that ((√2))^2 +((√3))^2 = 5 thank you sir shikari and this method can be used to find the square root of complex numbers very simple

$$\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}}\:=\:\sqrt{\mathrm{6}}\:=\:\sqrt{\mathrm{2}}×\sqrt{\mathrm{3}} \\ $$$${such}\:{that}\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:=\:\mathrm{5} \\ $$$${thank}\:{you}\:{sir}\:{shikari} \\ $$$${and}\:{this}\:{method}\:{can}\:{be}\:{used} \\ $$$${to}\:{find}\:{the}\:{square}\:{root}\:{of} \\ $$$${complex}\:{numbers}\: \\ $$$${very}\:{simple} \\ $$

Commented by Dwaipayan Shikari last updated on 26/Feb/21

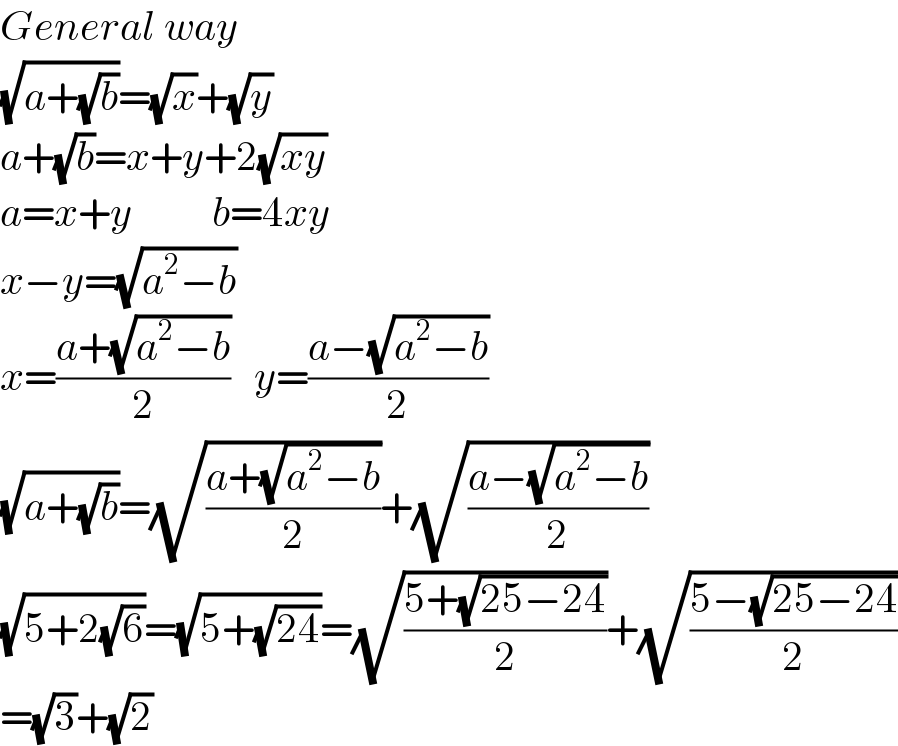
General way (√(a+(√b)))=(√x)+(√y) a+(√b)=x+y+2(√(xy)) a=x+y b=4xy x−y=(√(a^2 −b)) x=((a+(√(a^2 −b)))/2) y=((a−(√(a^2 −b)))/2) (√(a+(√b)))=(√((a+(√(a^2 −b)))/2))+(√((a−(√(a^2 −b)))/2)) (√(5+2(√6)))=(√(5+(√(24))))=(√((5+(√(25−24)))/2))+(√((5−(√(25−24)))/2)) =(√3)+(√2)

$${General}\:{way} \\ $$$$\sqrt{{a}+\sqrt{{b}}}=\sqrt{{x}}+\sqrt{{y}} \\ $$$${a}+\sqrt{{b}}={x}+{y}+\mathrm{2}\sqrt{{xy}} \\ $$$${a}={x}+{y}\:\:\:\:\:\:\:\:\:\:{b}=\mathrm{4}{xy} \\ $$$${x}−{y}=\sqrt{{a}^{\mathrm{2}} −{b}} \\ $$$${x}=\frac{{a}+\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}\:\:\:{y}=\frac{{a}−\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}\:\:\: \\ $$$$\sqrt{{a}+\sqrt{{b}}}=\sqrt{\frac{{a}+\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}}+\sqrt{\frac{{a}−\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}=\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}=\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{25}−\mathrm{24}}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{25}−\mathrm{24}}}{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}} \\ $$

Answered by malwan last updated on 26/Feb/21

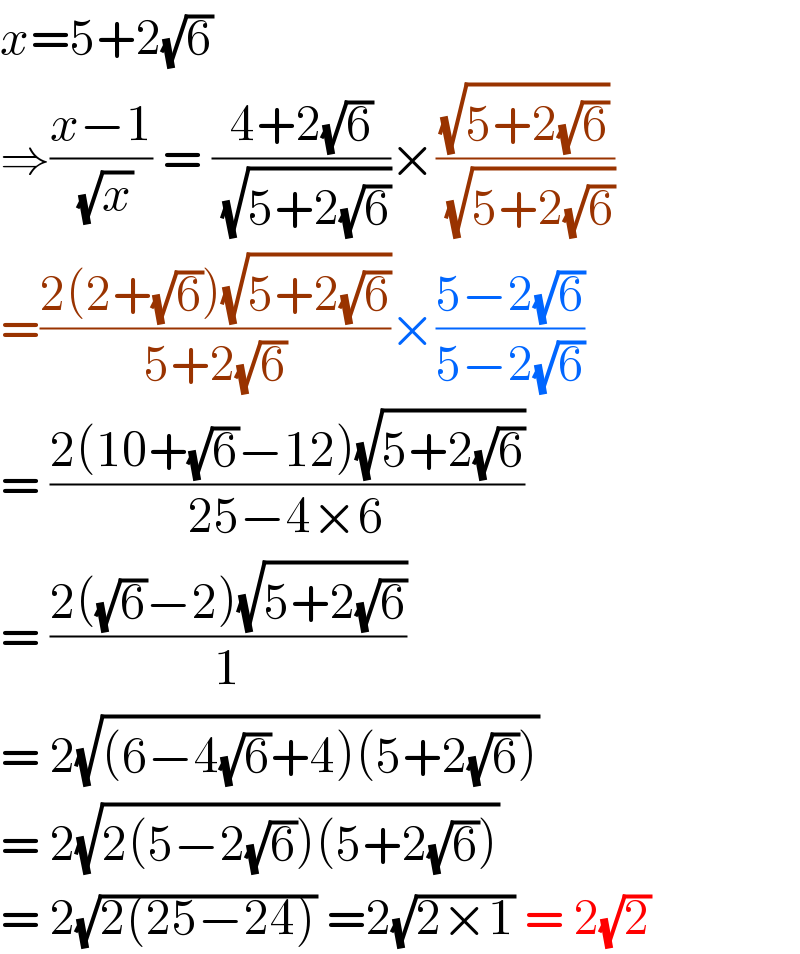
x=5+2(√6) ⇒((x−1)/( (√x))) = ((4+2(√6))/( (√(5+2(√6)))))×((√(5+2(√6)))/( (√(5+2(√6))))) =((2(2+(√6))(√(5+2(√6))))/(5+2(√6)))×((5−2(√6))/(5−2(√6))) = ((2(10+(√6)−12)(√(5+2(√6))))/(25−4×6)) = ((2((√6)−2)(√(5+2(√6))))/1) = 2(√((6−4(√6)+4)(5+2(√6)))) = 2(√(2(5−2(√6))(5+2(√6)))) = 2(√(2(25−24))) =2(√(2×1)) = 2(√2)

$${x}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\frac{{x}−\mathrm{1}}{\:\sqrt{{x}}}\:=\:\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}×\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}{\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}×\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$=\:\frac{\mathrm{2}\left(\mathrm{10}+\sqrt{\mathrm{6}}−\mathrm{12}\right)\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}{\mathrm{25}−\mathrm{4}×\mathrm{6}} \\ $$$$=\:\frac{\mathrm{2}\left(\sqrt{\mathrm{6}}−\mathrm{2}\right)\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}{\mathrm{1}} \\ $$$$=\:\mathrm{2}\sqrt{\left(\mathrm{6}−\mathrm{4}\sqrt{\mathrm{6}}+\mathrm{4}\right)\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{25}−\mathrm{24}\right)}\:=\mathrm{2}\sqrt{\mathrm{2}×\mathrm{1}}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com