
Question Number 209240 by Jubr last updated on 05/Jul/24
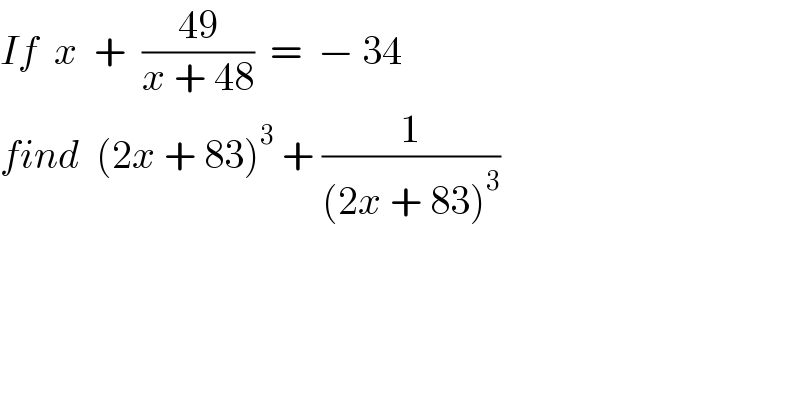
$${If}\:\:{x}\:\:+\:\:\frac{\mathrm{49}}{{x}\:+\:\mathrm{48}}\:\:=\:\:−\:\mathrm{34} \\ $$$${find}\:\:\left(\mathrm{2}{x}\:+\:\mathrm{83}\right)^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{\left(\mathrm{2}{x}\:+\:\mathrm{83}\right)^{\mathrm{3}} } \\ $$
Answered by som(math1967) last updated on 05/Jul/24
![x+48+((49)/(x+48))=−34+48 ⇒ a+((49)/a)=14 [let x+48=a] ⇒a^2 −14a+49=0 ⇒(a−7)^2 =0 ∴a=7 ⇒x+48=7 ⇒x=−41 ⇒2x=−82 ⇒2x+83=1 ∴(2x+83)+(1/((2x+83)))=1+1 y+(1/y)=2 [let (2x+83)=y] (y+(1/y))^3 =8 ⇒y^3 +(1/y^3 ) +3.y.(1/y)(y+(1/y))=8 ⇒y^3 +(1/y^3 )=8−3×2=2 ∴(2x+83)^3 +(1/((2x+83)^3 ))=2](Q209244.png)
$${x}+\mathrm{48}+\frac{\mathrm{49}}{{x}+\mathrm{48}}=−\mathrm{34}+\mathrm{48} \\ $$$$\Rightarrow\:{a}+\frac{\mathrm{49}}{{a}}=\mathrm{14}\:\left[{let}\:{x}+\mathrm{48}={a}\right] \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\mathrm{14}{a}+\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow\left({a}−\mathrm{7}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore{a}=\mathrm{7} \\ $$$$\Rightarrow{x}+\mathrm{48}=\mathrm{7} \\ $$$$\Rightarrow{x}=−\mathrm{41} \\ $$$$\Rightarrow\mathrm{2}{x}=−\mathrm{82} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{83}=\mathrm{1} \\ $$$$\therefore\left(\mathrm{2}{x}+\mathrm{83}\right)+\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{83}\right)}=\mathrm{1}+\mathrm{1} \\ $$$$\:{y}+\frac{\mathrm{1}}{{y}}=\mathrm{2}\:\:\left[{let}\:\left(\mathrm{2}{x}+\mathrm{83}\right)={y}\right] \\ $$$$\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{3}} =\mathrm{8} \\ $$$$\Rightarrow{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\:+\mathrm{3}.{y}.\frac{\mathrm{1}}{{y}}\left({y}+\frac{\mathrm{1}}{{y}}\right)=\mathrm{8} \\ $$$$\Rightarrow{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}^{\mathrm{3}} }=\mathrm{8}−\mathrm{3}×\mathrm{2}=\mathrm{2} \\ $$$$\therefore\left(\mathrm{2}{x}+\mathrm{83}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{83}\right)^{\mathrm{3}} }=\mathrm{2} \\ $$
Commented by Frix last updated on 05/Jul/24
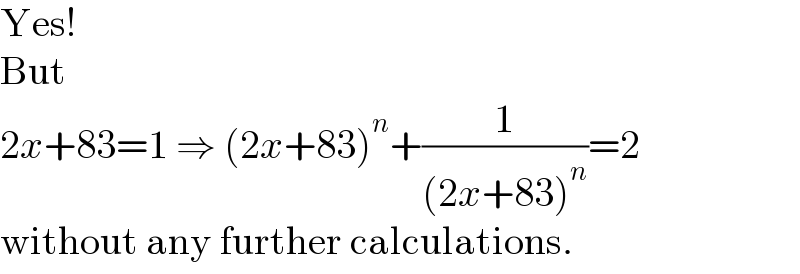
$$\mathrm{Yes}! \\ $$$$\mathrm{But} \\ $$$$\mathrm{2}{x}+\mathrm{83}=\mathrm{1}\:\Rightarrow\:\left(\mathrm{2}{x}+\mathrm{83}\right)^{{n}} +\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{83}\right)^{{n}} }=\mathrm{2} \\ $$$$\mathrm{without}\:\mathrm{any}\:\mathrm{further}\:\mathrm{calculations}. \\ $$
Commented by Spillover last updated on 05/Jul/24

$${perfect} \\ $$
Commented by Tawa11 last updated on 05/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
