
Question Number 6370 by sanusihammed last updated on 25/Jun/16
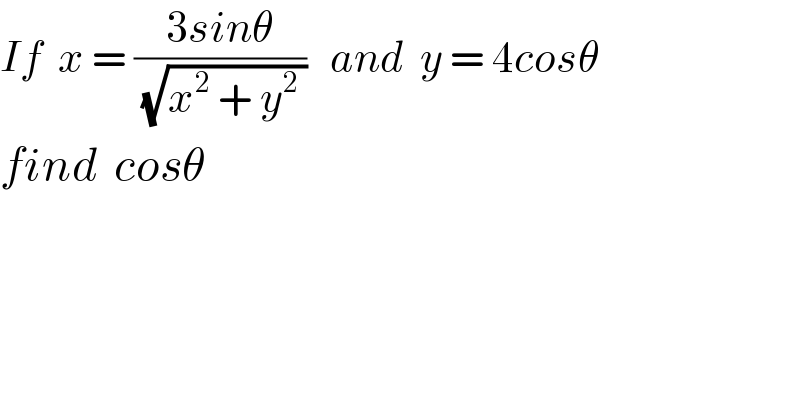
$${If}\:\:{x}\:=\:\frac{\mathrm{3}{sin}\theta}{\sqrt{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:}}\:\:\:{and}\:\:{y}\:=\:\mathrm{4}{cos}\theta \\ $$$${find}\:\:{cos}\theta \\ $$
Commented by nburiburu last updated on 25/Jun/16
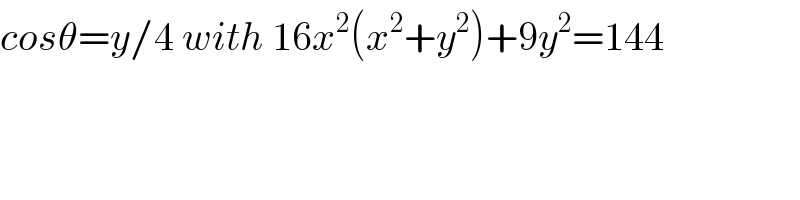
$${cos}\theta={y}/\mathrm{4}\:{with}\:\mathrm{16}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{9}{y}^{\mathrm{2}} =\mathrm{144} \\ $$
Commented by sanusihammed last updated on 25/Jun/16
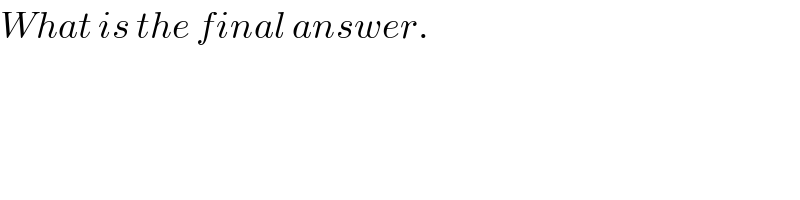
$${What}\:{is}\:{the}\:{final}\:{answer}. \\ $$
Commented by prakash jain last updated on 25/Jun/16

$$\mathrm{sin}\:\theta={a} \\ $$$$\mathrm{cos}\:\theta={b} \\ $$$$\mathrm{You}\:\mathrm{have}\:\mathrm{followinh}\:\mathrm{equations} \\ $$$${x}=\frac{\mathrm{3}{a}}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$${y}=\mathrm{4}{b} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{So}\:\mathrm{with}\:\mathrm{4}\:\mathrm{variables}\:\mathrm{you}\:\mathrm{have}\:\mathrm{only}\:\mathrm{3}\:\mathrm{equations}. \\ $$$$\mathrm{The}\:\mathrm{information}\:\mathrm{is}\:\mathrm{not}\:\mathrm{complete}. \\ $$
Commented by FilupSmith last updated on 25/Jun/16
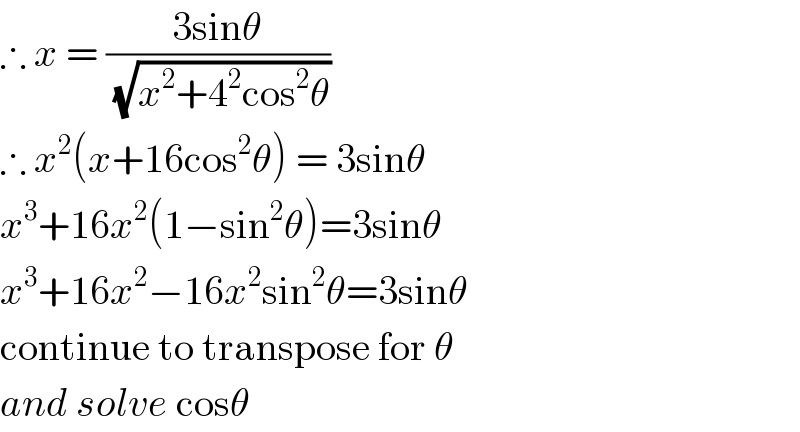
$$\therefore\:{x}\:=\:\frac{\mathrm{3sin}\theta}{\sqrt{{x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta}} \\ $$$$\therefore\:{x}^{\mathrm{2}} \left({x}+\mathrm{16cos}^{\mathrm{2}} \theta\right)\:=\:\mathrm{3sin}\theta \\ $$$${x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)=\mathrm{3sin}\theta \\ $$$${x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{2}} −\mathrm{16}{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta=\mathrm{3sin}\theta \\ $$$$\mathrm{continue}\:\mathrm{to}\:\mathrm{transpose}\:\mathrm{for}\:\theta \\ $$$${and}\:{solve}\:\mathrm{cos}\theta \\ $$
