
Question Number 205990 by MATHEMATICSAM last updated on 04/Apr/24
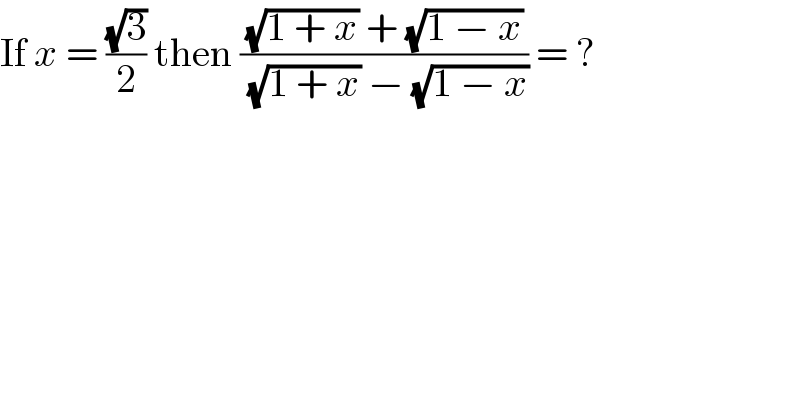
$$\mathrm{If}\:{x}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{then}\:\frac{\sqrt{\mathrm{1}\:+\:{x}}\:+\:\sqrt{\mathrm{1}\:−\:{x}}}{\:\sqrt{\mathrm{1}\:+\:{x}}\:−\:\sqrt{\mathrm{1}\:−\:{x}}}\:=\:? \\ $$
Answered by cortano12 last updated on 04/Apr/24
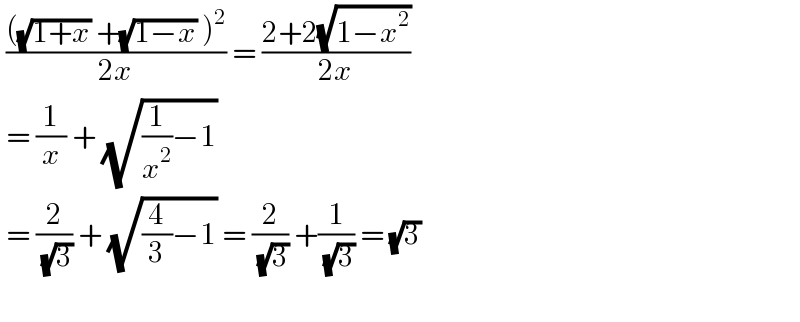
$$\:\frac{\left(\sqrt{\mathrm{1}+{x}}\:+\sqrt{\mathrm{1}−{x}}\:\right)^{\mathrm{2}} }{\mathrm{2}{x}}\:=\:\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}}\: \\ $$$$\:=\:\frac{\mathrm{1}}{{x}}\:+\:\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}\: \\ $$$$\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:+\:\sqrt{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{1}}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:=\:\sqrt{\mathrm{3}} \\ $$$$ \\ $$
Answered by Berbere last updated on 04/Apr/24
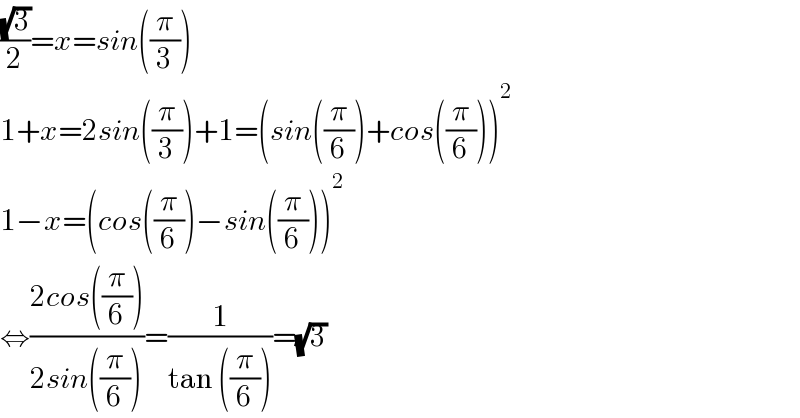
$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={x}={sin}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{1}+{x}=\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{3}}\right)+\mathrm{1}=\left({sin}\left(\frac{\pi}{\mathrm{6}}\right)+{cos}\left(\frac{\pi}{\mathrm{6}}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−{x}=\left({cos}\left(\frac{\pi}{\mathrm{6}}\right)−{sin}\left(\frac{\pi}{\mathrm{6}}\right)\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{6}}\right)}=\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{6}}\right)}=\sqrt{\mathrm{3}} \\ $$
