
Question Number 138469 by KwesiDerek last updated on 13/Apr/21
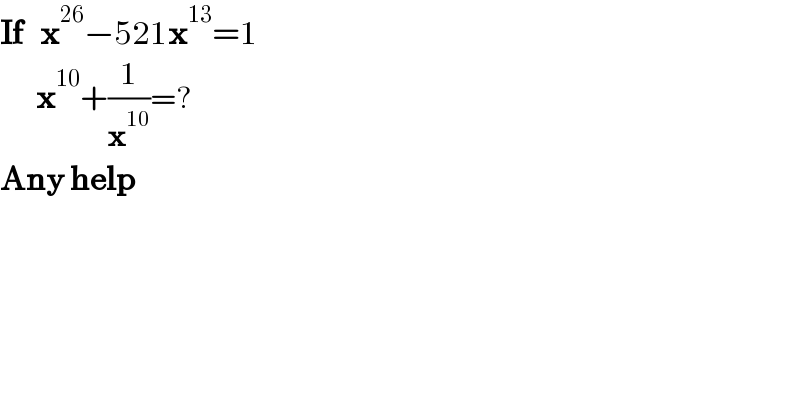
$$\boldsymbol{\mathrm{If}}\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{26}} −\mathrm{521}\boldsymbol{\mathrm{x}}^{\mathrm{13}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{10}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{10}} }=? \\ $$$$\boldsymbol{\mathrm{Any}}\:\boldsymbol{\mathrm{help}}\: \\ $$
Answered by MJS_new last updated on 14/Apr/21
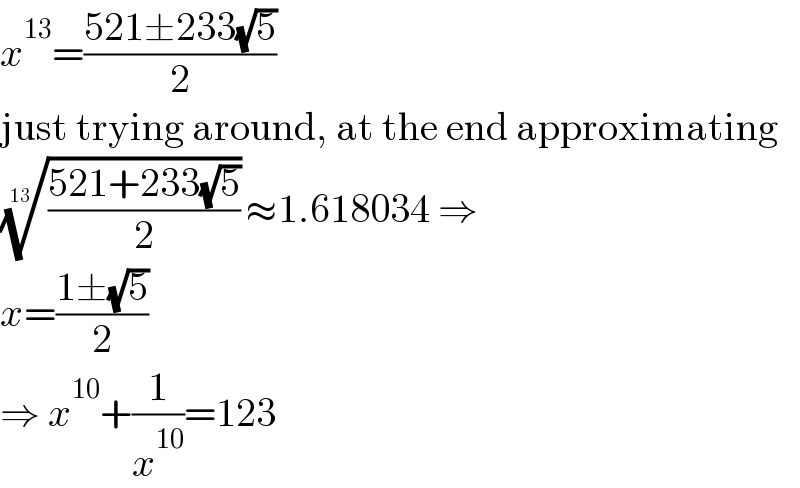
$${x}^{\mathrm{13}} =\frac{\mathrm{521}\pm\mathrm{233}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{just}\:\mathrm{trying}\:\mathrm{around},\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}\:\mathrm{approximating} \\ $$$$\sqrt[{\mathrm{13}}]{\frac{\mathrm{521}+\mathrm{233}\sqrt{\mathrm{5}}}{\mathrm{2}}}\approx\mathrm{1}.\mathrm{618034}\:\Rightarrow \\ $$$${x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}^{\mathrm{10}} +\frac{\mathrm{1}}{{x}^{\mathrm{10}} }=\mathrm{123} \\ $$
Answered by TheSupreme last updated on 14/Apr/21
![x^(13) =t t^2 −521t+1=0 → t=((521±(√(521^2 −4)))/2) x^(10) =t^((10)/(13)) x^(10) +(1/x^(10) )=[((521±(√(521^2 −4)))/2)]^((10)/(13)) +[(2/(521±(√(521^2 −4))))]^((10)/(13))](Q138487.png)
$${x}^{\mathrm{13}} ={t} \\ $$$${t}^{\mathrm{2}} −\mathrm{521}{t}+\mathrm{1}=\mathrm{0}\:\rightarrow\:{t}=\frac{\mathrm{521}\pm\sqrt{\mathrm{521}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{10}} ={t}^{\frac{\mathrm{10}}{\mathrm{13}}} \\ $$$${x}^{\mathrm{10}} +\frac{\mathrm{1}}{{x}^{\mathrm{10}} }=\left[\frac{\mathrm{521}\pm\sqrt{\mathrm{521}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right]^{\frac{\mathrm{10}}{\mathrm{13}}} +\left[\frac{\mathrm{2}}{\mathrm{521}\pm\sqrt{\mathrm{521}^{\mathrm{2}} −\mathrm{4}}}\right]^{\frac{\mathrm{10}}{\mathrm{13}}} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Apr/21
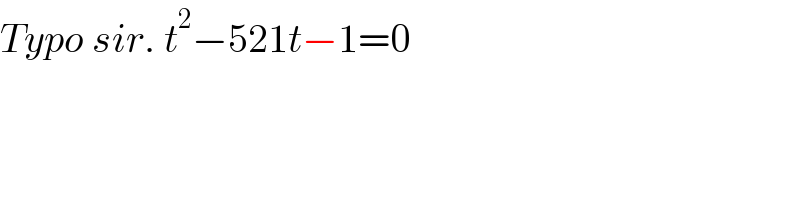
$${Typo}\:{sir}.\:{t}^{\mathrm{2}} −\mathrm{521}{t}−\mathrm{1}=\mathrm{0} \\ $$
