Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 203245 by hardmath last updated on 13/Jan/24

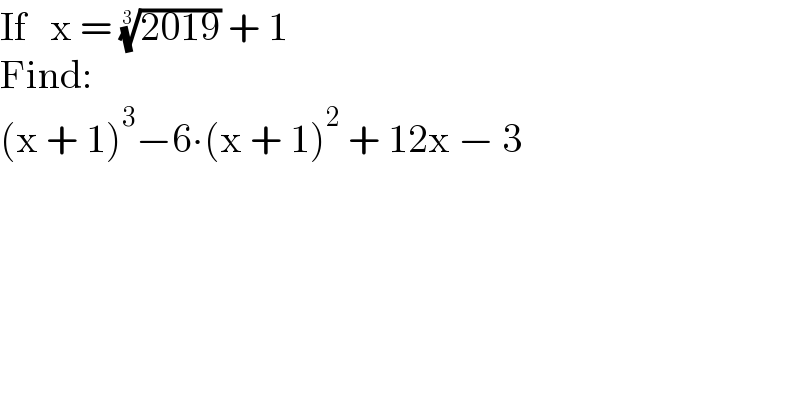
If x = ((2019))^(1/3) + 1 Find: (x + 1)^3 −6∙(x + 1)^2 + 12x − 3

$$\mathrm{If}\:\:\:\mathrm{x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2019}}\:+\:\mathrm{1} \\ $$$$\mathrm{Find}: \\ $$$$\left(\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{3}} −\mathrm{6}\centerdot\left(\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:+\:\mathrm{12x}\:−\:\mathrm{3} \\ $$

Answered by mr W last updated on 13/Jan/24

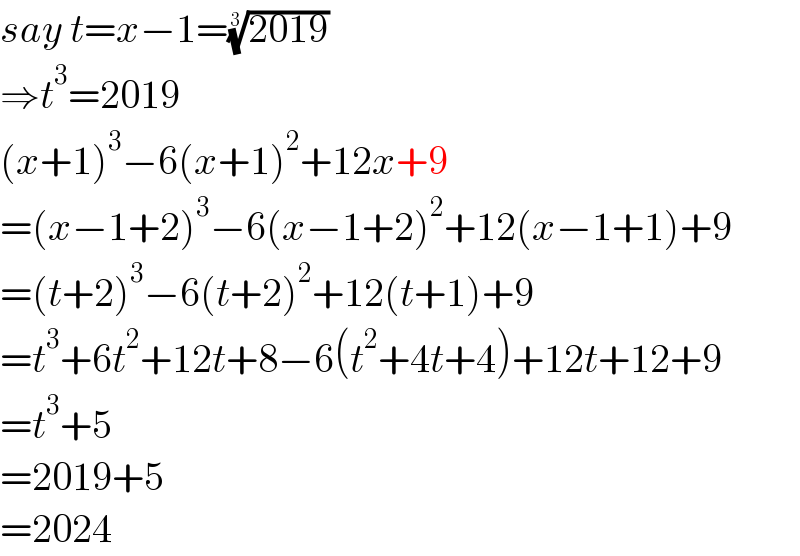
say t=x−1=((2019))^(1/3) ⇒t^3 =2019 (x+1)^3 −6(x+1)^2 +12x+9 =(x−1+2)^3 −6(x−1+2)^2 +12(x−1+1)+9 =(t+2)^3 −6(t+2)^2 +12(t+1)+9 =t^3 +6t^2 +12t+8−6(t^2 +4t+4)+12t+12+9 =t^3 +5 =2019+5 =2024

$${say}\:{t}={x}−\mathrm{1}=\sqrt[{\mathrm{3}}]{\mathrm{2019}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} =\mathrm{2019} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{6}\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9} \\ $$$$=\left({x}−\mathrm{1}+\mathrm{2}\right)^{\mathrm{3}} −\mathrm{6}\left({x}−\mathrm{1}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{12}\left({x}−\mathrm{1}+\mathrm{1}\right)+\mathrm{9} \\ $$$$=\left({t}+\mathrm{2}\right)^{\mathrm{3}} −\mathrm{6}\left({t}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{12}\left({t}+\mathrm{1}\right)+\mathrm{9} \\ $$$$={t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} +\mathrm{12}{t}+\mathrm{8}−\mathrm{6}\left({t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{4}\right)+\mathrm{12}{t}+\mathrm{12}+\mathrm{9} \\ $$$$={t}^{\mathrm{3}} +\mathrm{5} \\ $$$$=\mathrm{2019}+\mathrm{5} \\ $$$$=\mathrm{2024} \\ $$

Commented by hardmath last updated on 13/Jan/24

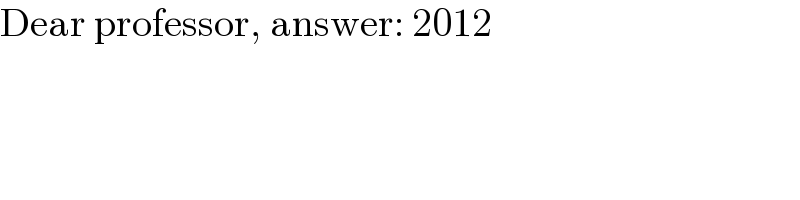
Dear professor, answer: 2012

$$\mathrm{Dear}\:\mathrm{professor},\:\mathrm{answer}:\:\mathrm{2012} \\ $$

Commented by mr W last updated on 13/Jan/24

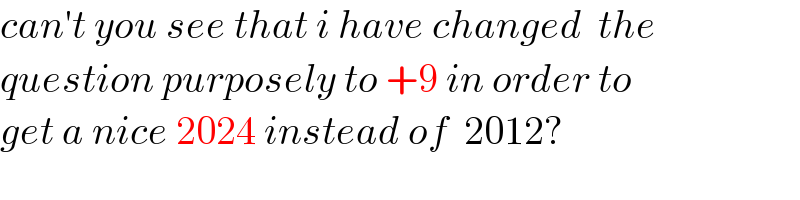
can′t you see that i have changed the question purposely to +9 in order to get a nice 2024 instead of 2012?

$${can}'{t}\:{you}\:{see}\:{that}\:{i}\:{have}\:{changed}\:\:{the} \\ $$$${question}\:{purposely}\:{to}\:+\mathrm{9}\:{in}\:{order}\:{to} \\ $$$${get}\:{a}\:{nice}\:\mathrm{2024}\:{instead}\:{of}\:\:\mathrm{2012}? \\ $$

Answered by Rasheed.Sindhi last updated on 13/Jan/24

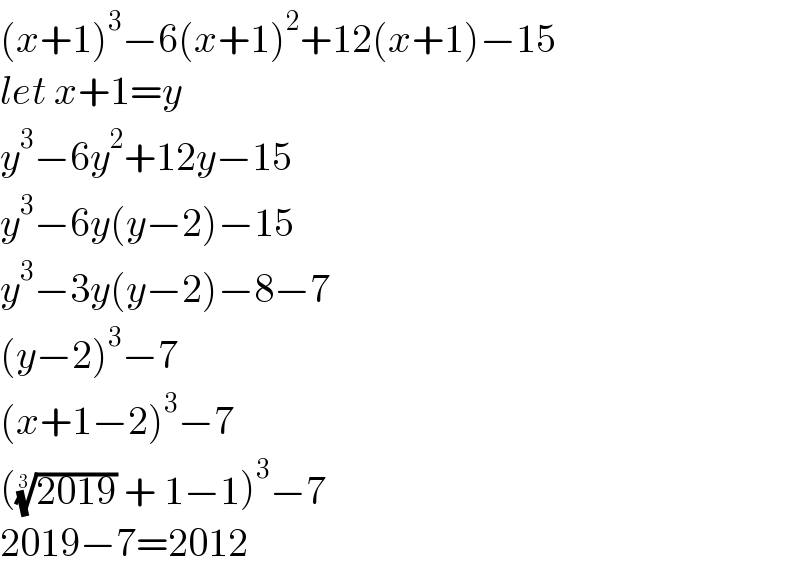
(x+1)^3 −6(x+1)^2 +12(x+1)−15 let x+1=y y^3 −6y^2 +12y−15 y^3 −6y(y−2)−15 y^3 −3y(y−2)−8−7 (y−2)^3 −7 (x+1−2)^3 −7 (((2019))^(1/3) + 1−1)^3 −7 2019−7=2012

$$\left({x}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{6}\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{12}\left({x}+\mathrm{1}\right)−\mathrm{15} \\ $$$${let}\:{x}+\mathrm{1}={y} \\ $$$${y}^{\mathrm{3}} −\mathrm{6}{y}^{\mathrm{2}} +\mathrm{12}{y}−\mathrm{15} \\ $$$${y}^{\mathrm{3}} −\mathrm{6}{y}\left({y}−\mathrm{2}\right)−\mathrm{15} \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}\left({y}−\mathrm{2}\right)−\mathrm{8}−\mathrm{7} \\ $$$$\left({y}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{7} \\ $$$$\left({x}+\mathrm{1}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{7} \\ $$$$\left(\sqrt[{\mathrm{3}}]{\mathrm{2019}}\:+\:\mathrm{1}−\mathrm{1}\right)^{\mathrm{3}} −\mathrm{7} \\ $$$$\mathrm{2019}−\mathrm{7}=\mathrm{2012} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Jan/24

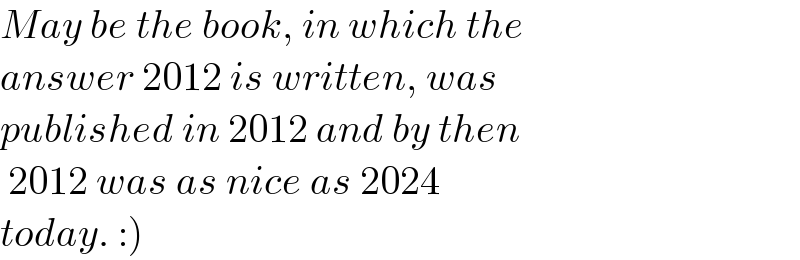
May be the book, in which the answer 2012 is written, was published in 2012 and by then 2012 was as nice as 2024 today. :)

$${May}\:{be}\:{the}\:{book},\:{in}\:{which}\:{the} \\ $$$${answer}\:\mathrm{2012}\:{is}\:{written},\:{was}\: \\ $$$${published}\:{in}\:\mathrm{2012}\:{and}\:{by}\:{then} \\ $$$$\:\mathrm{2012}\:{was}\:{as}\:{nice}\:{as}\:\mathrm{2024} \\ $$$$\left.{today}.\::\right) \\ $$

Commented by hardmath last updated on 13/Jan/24

My dear professors, I think years are not important)

$$\mathrm{My}\:\mathrm{dear}\:\mathrm{professors}, \\ $$$$ \\ $$I think years are not important)

Terms of Service

Privacy Policy

Contact: info@tinkutara.com