Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139490 by EnterUsername last updated on 27/Apr/21

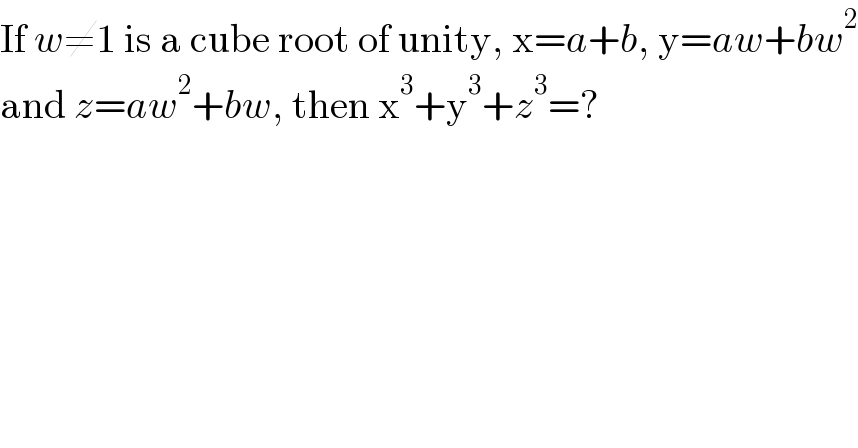
If w≠1 is a cube root of unity, x=a+b, y=aw+bw^2 and z=aw^2 +bw, then x^3 +y^3 +z^3 =?

$$\mathrm{If}\:{w}\neq\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity},\:\mathrm{x}={a}+{b},\:\mathrm{y}={aw}+{bw}^{\mathrm{2}} \\ $$$$\mathrm{and}\:{z}={aw}^{\mathrm{2}} +{bw},\:\mathrm{then}\:\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =? \\ $$

Answered by Rasheed.Sindhi last updated on 27/Apr/21

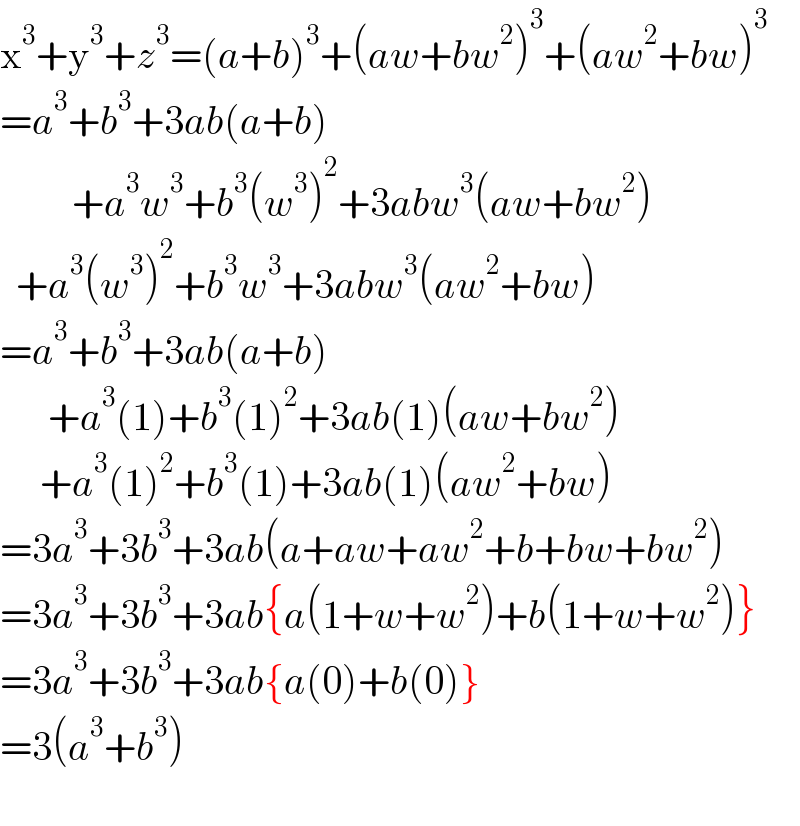
x^3 +y^3 +z^3 =(a+b)^3 +(aw+bw^2 )^3 +(aw^2 +bw)^3 =a^3 +b^3 +3ab(a+b) +a^3 w^3 +b^3 (w^3 )^2 +3abw^3 (aw+bw^2 ) +a^3 (w^3 )^2 +b^3 w^3 +3abw^3 (aw^2 +bw) =a^3 +b^3 +3ab(a+b) +a^3 (1)+b^3 (1)^2 +3ab(1)(aw+bw^2 ) +a^3 (1)^2 +b^3 (1)+3ab(1)(aw^2 +bw) =3a^3 +3b^3 +3ab(a+aw+aw^2 +b+bw+bw^2 ) =3a^3 +3b^3 +3ab{a(1+w+w^2 )+b(1+w+w^2 )} =3a^3 +3b^3 +3ab{a(0)+b(0)} =3(a^3 +b^3 )

$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\left({a}+{b}\right)^{\mathrm{3}} +\left({aw}+{bw}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({aw}^{\mathrm{2}} +{bw}\right)^{\mathrm{3}} \\ $$$$={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:+{a}^{\mathrm{3}} {w}^{\mathrm{3}} +{b}^{\mathrm{3}} \left({w}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{3}{abw}^{\mathrm{3}} \left({aw}+{bw}^{\mathrm{2}} \right) \\ $$$$\:\:+{a}^{\mathrm{3}} \left({w}^{\mathrm{3}} \right)^{\mathrm{2}} +{b}^{\mathrm{3}} {w}^{\mathrm{3}} +\mathrm{3}{abw}^{\mathrm{3}} \left({aw}^{\mathrm{2}} +{bw}\right) \\ $$$$={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$\:\:\:\:\:\:+{a}^{\mathrm{3}} \left(\mathrm{1}\right)+{b}^{\mathrm{3}} \left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{ab}\left(\mathrm{1}\right)\left({aw}+{bw}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:+{a}^{\mathrm{3}} \left(\mathrm{1}\right)^{\mathrm{2}} +{b}^{\mathrm{3}} \left(\mathrm{1}\right)+\mathrm{3}{ab}\left(\mathrm{1}\right)\left({aw}^{\mathrm{2}} +{bw}\right) \\ $$$$=\mathrm{3}{a}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{aw}+{aw}^{\mathrm{2}} +{b}+{bw}+{bw}^{\mathrm{2}} \right) \\ $$$$=\mathrm{3}{a}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{3}} +\mathrm{3}{ab}\left\{{a}\left(\mathrm{1}+{w}+{w}^{\mathrm{2}} \right)+{b}\left(\mathrm{1}+{w}+{w}^{\mathrm{2}} \right)\right\} \\ $$$$=\mathrm{3}{a}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{3}} +\mathrm{3}{ab}\left\{{a}\left(\mathrm{0}\right)+{b}\left(\mathrm{0}\right)\right\} \\ $$$$=\mathrm{3}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} \right) \\ $$$$ \\ $$

Commented by EnterUsername last updated on 27/Apr/21

Thanks Sir

$${Thanks}\:{Sir} \\ $$

Answered by Ar Brandon last updated on 27/Apr/21

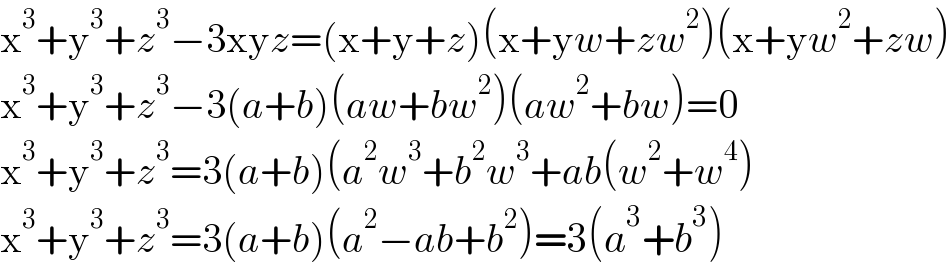
x^3 +y^3 +z^3 −3xyz=(x+y+z)(x+yw+zw^2 )(x+yw^2 +zw) x^3 +y^3 +z^3 −3(a+b)(aw+bw^2 )(aw^2 +bw)=0 x^3 +y^3 +z^3 =3(a+b)(a^2 w^3 +b^2 w^3 +ab(w^2 +w^4 ) x^3 +y^3 +z^3 =3(a+b)(a^2 −ab+b^2 )=3(a^3 +b^3 )

$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3xy}{z}=\left(\mathrm{x}+\mathrm{y}+{z}\right)\left(\mathrm{x}+\mathrm{y}{w}+{zw}^{\mathrm{2}} \right)\left(\mathrm{x}+\mathrm{y}{w}^{\mathrm{2}} +{zw}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}\left({a}+{b}\right)\left({aw}+{bw}^{\mathrm{2}} \right)\left({aw}^{\mathrm{2}} +{bw}\right)=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{3}\left({a}+{b}\right)\left({a}^{\mathrm{2}} {w}^{\mathrm{3}} +{b}^{\mathrm{2}} {w}^{\mathrm{3}} +{ab}\left({w}^{\mathrm{2}} +{w}^{\mathrm{4}} \right)\right. \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{3}\left({a}+{b}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)=\mathrm{3}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} \right) \\ $$

Commented by Ar Brandon last updated on 27/Apr/21

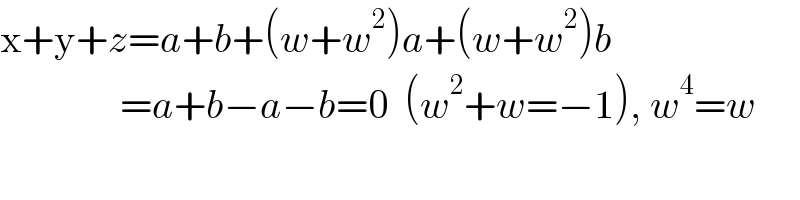
x+y+z=a+b+(w+w^2 )a+(w+w^2 )b =a+b−a−b=0 (w^2 +w=−1), w^4 =w

$$\mathrm{x}+\mathrm{y}+{z}={a}+{b}+\left({w}+{w}^{\mathrm{2}} \right){a}+\left({w}+{w}^{\mathrm{2}} \right){b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}+{b}−{a}−{b}=\mathrm{0}\:\:\left({w}^{\mathrm{2}} +{w}=−\mathrm{1}\right),\:{w}^{\mathrm{4}} ={w} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com