
Question Number 135935 by Engr_Jidda last updated on 17/Mar/21
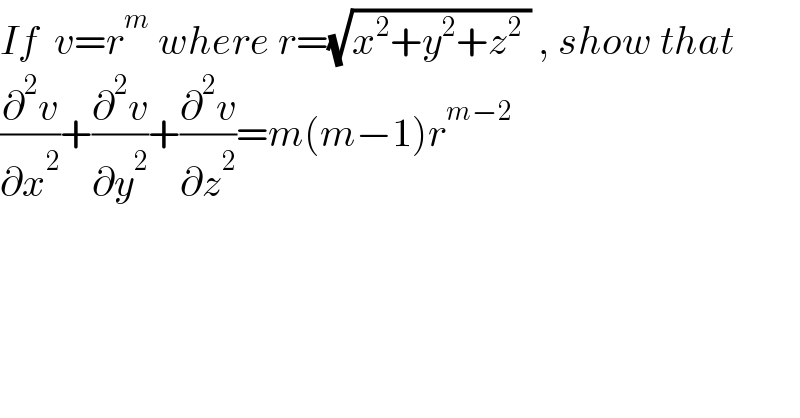
$${If}\:\:{v}={r}^{{m}} \:{where}\:{r}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:}\:,\:{show}\:{that} \\ $$$$\frac{\partial^{\mathrm{2}} {v}}{\partial{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} {v}}{\partial{y}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} {v}}{\partial{z}^{\mathrm{2}} }={m}\left({m}−\mathrm{1}\right){r}^{{m}−\mathrm{2}} \\ $$
Answered by Olaf last updated on 17/Mar/21
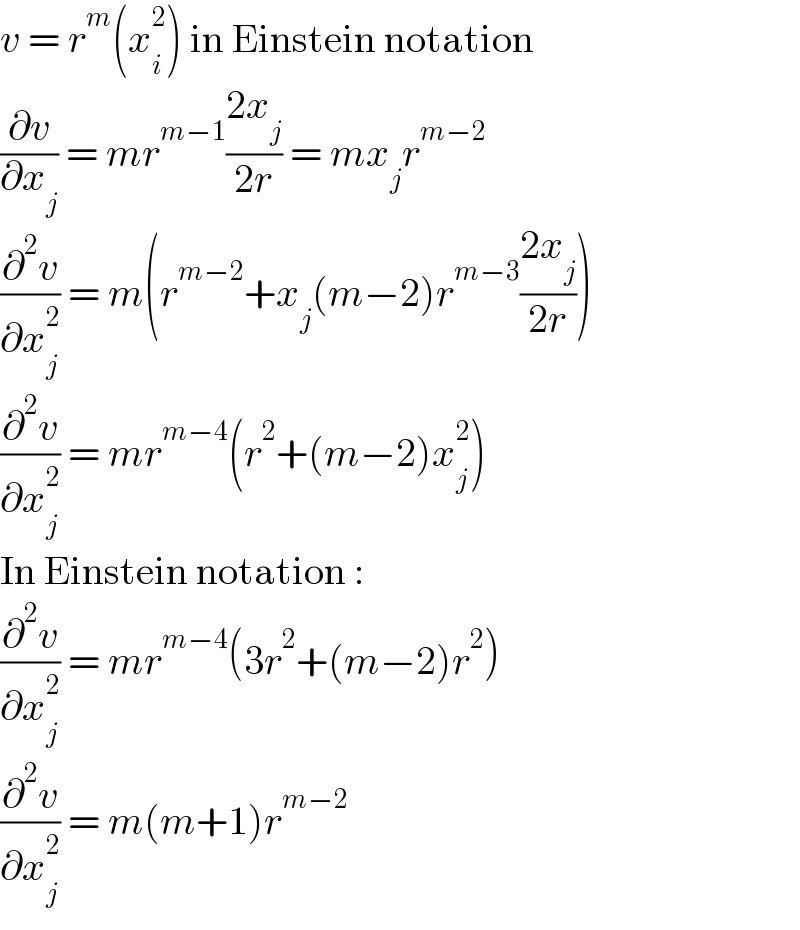
$${v}\:=\:{r}^{{m}} \left({x}_{{i}} ^{\mathrm{2}} \right)\:\mathrm{in}\:\mathrm{Einstein}\:\mathrm{notation} \\ $$$$\frac{\partial{v}}{\partial{x}_{{j}} }\:=\:{mr}^{{m}−\mathrm{1}} \frac{\mathrm{2}{x}_{{j}} }{\mathrm{2}{r}}\:=\:{mx}_{{j}} {r}^{{m}−\mathrm{2}} \\ $$$$\frac{\partial^{\mathrm{2}} {v}}{\partial{x}_{{j}} ^{\mathrm{2}} }\:=\:{m}\left({r}^{{m}−\mathrm{2}} +{x}_{{j}} \left({m}−\mathrm{2}\right){r}^{{m}−\mathrm{3}} \frac{\mathrm{2}{x}_{{j}} }{\mathrm{2}{r}}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {v}}{\partial{x}_{{j}} ^{\mathrm{2}} }\:=\:{mr}^{{m}−\mathrm{4}} \left({r}^{\mathrm{2}} +\left({m}−\mathrm{2}\right){x}_{{j}} ^{\mathrm{2}} \right) \\ $$$$\mathrm{In}\:\mathrm{Einstein}\:\mathrm{notation}\:: \\ $$$$\frac{\partial^{\mathrm{2}} {v}}{\partial{x}_{{j}} ^{\mathrm{2}} }\:=\:{mr}^{{m}−\mathrm{4}} \left(\mathrm{3}{r}^{\mathrm{2}} +\left({m}−\mathrm{2}\right){r}^{\mathrm{2}} \right) \\ $$$$\frac{\partial^{\mathrm{2}} {v}}{\partial{x}_{{j}} ^{\mathrm{2}} }\:=\:{m}\left({m}+\mathrm{1}\right){r}^{{m}−\mathrm{2}} \\ $$
