
Question Number 185695 by Spillover last updated on 25/Jan/23
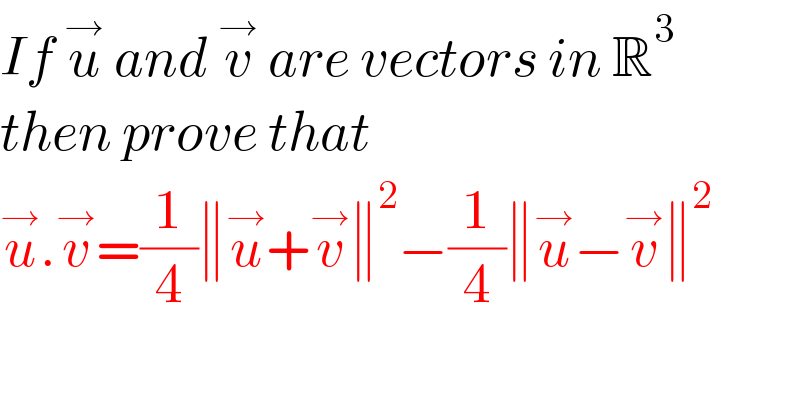
$${If}\:\overset{\rightarrow} {{u}}\:{and}\:\overset{\rightarrow} {{v}}\:{are}\:{vectors}\:{in}\:\mathbb{R}^{\mathrm{3}} \\ $$$${then}\:{prove}\:{that}\: \\ $$$$\overset{\rightarrow} {{u}}.\overset{\rightarrow} {{v}}=\frac{\mathrm{1}}{\mathrm{4}}\parallel\overset{\rightarrow} {{u}}+\overset{\rightarrow} {{v}}\parallel^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\parallel\overset{\rightarrow} {{u}}−\overset{\rightarrow} {{v}}\parallel^{\mathrm{2}} \\ $$
Answered by mahdipoor last updated on 26/Jan/23
![u=(a,b,c) v=(x,y,z) (1/4)∣∣u+v∣∣^2 −(1/4)∣∣u−v∣∣^2 = (1/4)[(a+x)^2 +(b+y)^2 +(c+z)^2 ]− (1/4)[(a−x)^2 +(b−y)^2 +(c−z)^2 ]= (1/4)[4ax+4by+4cz]=ax+by+cz=u.v](Q185707.png)
$${u}=\left({a},{b},{c}\right)\:\:\:\:\:\:\:{v}=\left({x},{y},{z}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mid\mid{u}+{v}\mid\mid^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\mid\mid{u}−{v}\mid\mid^{\mathrm{2}} = \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\left({a}+{x}\right)^{\mathrm{2}} +\left({b}+{y}\right)^{\mathrm{2}} +\left({c}+{z}\right)^{\mathrm{2}} \right]− \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\left({a}−{x}\right)^{\mathrm{2}} +\left({b}−{y}\right)^{\mathrm{2}} +\left({c}−{z}\right)^{\mathrm{2}} \right]= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{4}{ax}+\mathrm{4}{by}+\mathrm{4}{cz}\right]={ax}+{by}+{cz}={u}.{v} \\ $$
Answered by cortano1 last updated on 26/Jan/23
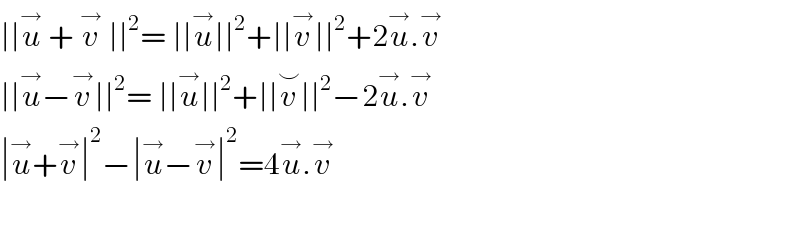
$$\mid\mid\overset{\rightarrow} {{u}}\:+\:\overset{\rightarrow} {{v}}\:\mid\mid^{\mathrm{2}} =\:\mid\mid\overset{\rightarrow} {{u}}\mid\mid^{\mathrm{2}} +\mid\mid\overset{\rightarrow} {{v}}\mid\mid^{\mathrm{2}} +\mathrm{2}\overset{\rightarrow} {{u}}.\overset{\rightarrow} {{v}} \\ $$$$\mid\mid\overset{\rightarrow} {{u}}−\overset{\rightarrow} {{v}}\mid\mid^{\mathrm{2}} =\:\mid\mid\overset{\rightarrow} {{u}}\mid\mid^{\mathrm{2}} +\mid\mid\overset{\smile} {{v}}\mid\mid^{\mathrm{2}} −\mathrm{2}\overset{\rightarrow} {{u}}.\overset{\rightarrow} {{v}} \\ $$$$\mid\overset{\rightarrow} {{u}}+\overset{\rightarrow} {{v}}\mid^{\mathrm{2}} −\mid\overset{\rightarrow} {{u}}−\overset{\rightarrow} {{v}}\mid^{\mathrm{2}} =\mathrm{4}\overset{\rightarrow} {{u}}.\overset{\rightarrow} {{v}} \\ $$$$ \\ $$
