Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 217909 by Tawa11 last updated on 23/Mar/25

If two fair dice is thrown twice, what is the probability of obtaining an even number

If two fair dice is thrown twice, what is the probability of obtaining an even number

Commented by mr W last updated on 24/Mar/25

p=1−((2×4)/2^4 )=(1/2)

$${p}=\mathrm{1}−\frac{\mathrm{2}×\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Unhombre last updated on 23/Mar/25

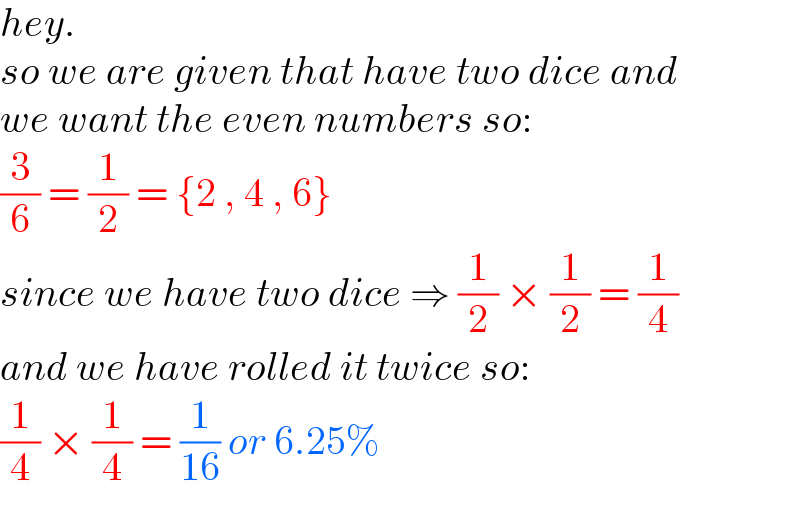
hey. so we are given that have two dice and we want the even numbers so: (3/6) = (1/2) = {2 , 4 , 6} since we have two dice ⇒ (1/2) × (1/2) = (1/4) and we have rolled it twice so: (1/4) × (1/4) = (1/(16)) or 6.25%

$${hey}. \\ $$$${so}\:{we}\:{are}\:{given}\:{that}\:{have}\:{two}\:{dice}\:{and} \\ $$$${we}\:{want}\:{the}\:{even}\:{numbers}\:{so}:\:\: \\ $$$$\frac{\mathrm{3}}{\mathrm{6}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\left\{\mathrm{2}\:,\:\mathrm{4}\:,\:\mathrm{6}\right\}\: \\ $$$${since}\:{we}\:{have}\:{two}\:{dice}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${and}\:{we}\:{have}\:{rolled}\:{it}\:{twice}\:{so}: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:×\:\frac{\mathrm{1}}{\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:{or}\:\mathrm{6}.\mathrm{25\%} \\ $$

Commented by Frix last updated on 23/Mar/25

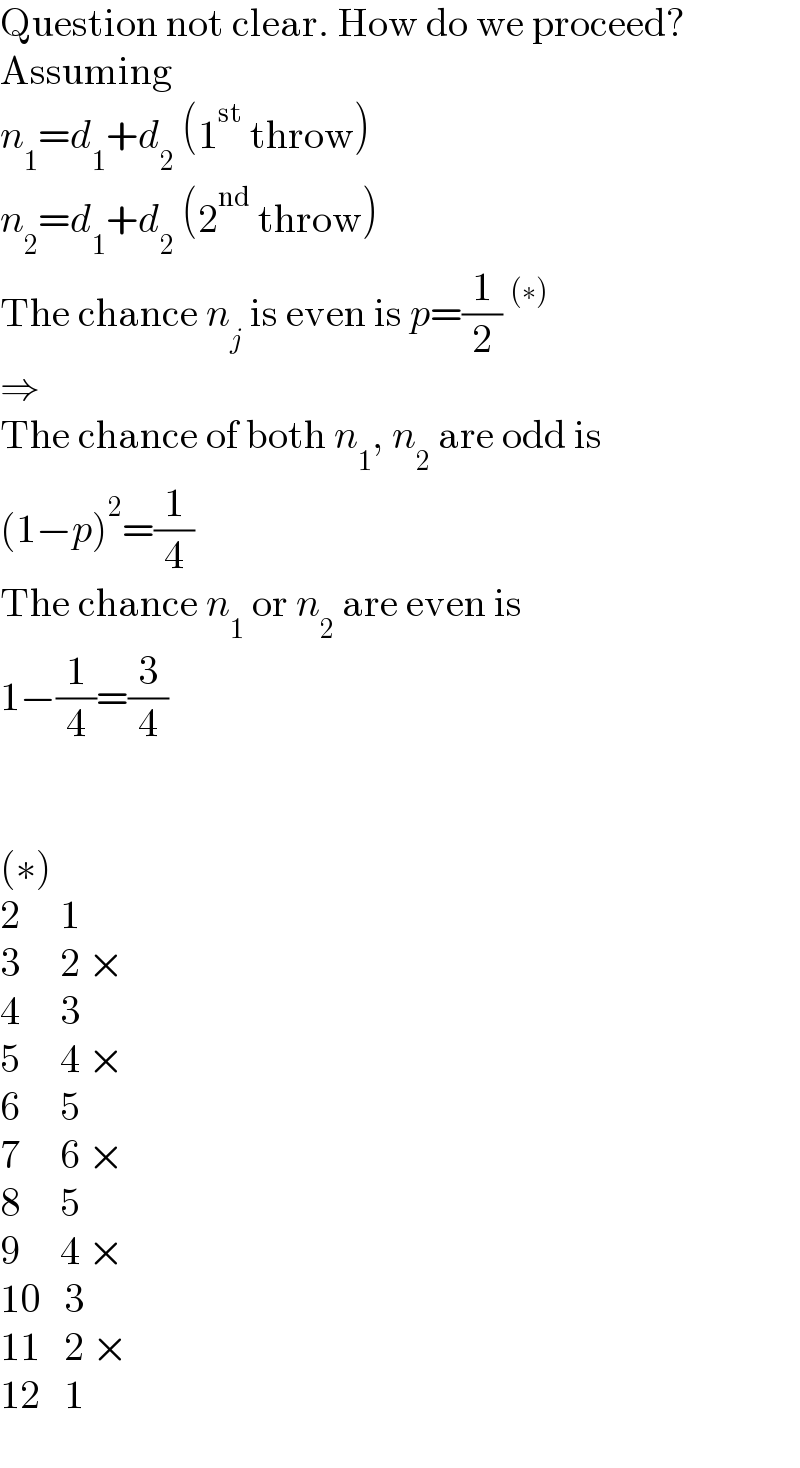
Question not clear. How do we proceed? Assuming n_1 =d_1 +d_2 (1^(st) throw) n_2 =d_1 +d_2 (2^(nd) throw) The chance n_j is even is p=(1/2)^((∗)) ⇒ The chance of both n_1 , n_2 are odd is (1−p)^2 =(1/4) The chance n_1 or n_2 are even is 1−(1/4)=(3/4) (∗) 2 1 3 2 × 4 3 5 4 × 6 5 7 6 × 8 5 9 4 × 10 3 11 2 × 12 1

$$\mathrm{Question}\:\mathrm{not}\:\mathrm{clear}.\:\mathrm{How}\:\mathrm{do}\:\mathrm{we}\:\mathrm{proceed}? \\ $$$$\mathrm{Assuming} \\ $$$${n}_{\mathrm{1}} ={d}_{\mathrm{1}} +{d}_{\mathrm{2}} \:\left(\mathrm{1}^{\mathrm{st}} \:\mathrm{throw}\right) \\ $$$${n}_{\mathrm{2}} ={d}_{\mathrm{1}} +{d}_{\mathrm{2}} \:\left(\mathrm{2}^{\mathrm{nd}} \:\mathrm{throw}\right) \\ $$$$\mathrm{The}\:\mathrm{chance}\:{n}_{{j}} \:\mathrm{is}\:\mathrm{even}\:\mathrm{is}\:{p}=\frac{\mathrm{1}}{\mathrm{2}}\:^{\left(\ast\right)} \\ $$$$\Rightarrow \\ $$$$\mathrm{The}\:\mathrm{chance}\:\mathrm{of}\:\mathrm{both}\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{odd}\:\mathrm{is} \\ $$$$\left(\mathrm{1}−{p}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{The}\:\mathrm{chance}\:{n}_{\mathrm{1}} \:\mathrm{or}\:{n}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{even}\:\mathrm{is} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$\left(\ast\right) \\ $$$$\mathrm{2}\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{3}\:\:\:\:\:\mathrm{2}\:× \\ $$$$\mathrm{4}\:\:\:\:\:\mathrm{3} \\ $$$$\mathrm{5}\:\:\:\:\:\mathrm{4}\:× \\ $$$$\mathrm{6}\:\:\:\:\:\mathrm{5} \\ $$$$\mathrm{7}\:\:\:\:\:\mathrm{6}\:× \\ $$$$\mathrm{8}\:\:\:\:\:\mathrm{5} \\ $$$$\mathrm{9}\:\:\:\:\:\mathrm{4}\:× \\ $$$$\mathrm{10}\:\:\:\mathrm{3} \\ $$$$\mathrm{11}\:\:\:\mathrm{2}\:× \\ $$$$\mathrm{12}\:\:\:\mathrm{1} \\ $$

Commented by Frix last updated on 23/Mar/25

Dear Unhombre, you′re wrong. The chance to get an even number must be greater when you throw 4 dices...

$$\mathrm{Dear}\:\mathrm{Unhombre},\:\mathrm{you}'\mathrm{re}\:\mathrm{wrong}. \\ $$$$\mathrm{The}\:\mathrm{chance}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{even}\:\mathrm{number}\:\mathrm{must} \\ $$$$\mathrm{be}\:\mathrm{greater}\:\mathrm{when}\:\mathrm{you}\:\mathrm{throw}\:\mathrm{4}\:\mathrm{dices}... \\ $$

Commented by Unhombre last updated on 23/Mar/25

Hi dear Frix Well it is saying we have two dices and we throw it twice so I dont think I did something wrong could you please clarify where I did it wrong? Thank you

$${Hi}\:{dear}\:{Frix}\: \\ $$$${Well}\:{it}\:{is}\:{saying}\:{we}\:{have}\:{two}\:{dices}\:{and}\:{we}\: \\ $$$${throw}\:{it}\:{twice}\:{so}\:{I}\:{dont}\:{think}\:{I}\:{did}\: \\ $$$${something}\:{wrong} \\ $$$${could}\:{you}\:{please}\:{clarify}\:{where}\:{I}\:{did}\:{it} \\ $$$${wrong}? \\ $$$${Thank}\:{you} \\ $$

Commented by mr W last updated on 23/Mar/25

i also think that the question is not clear. what means “obtaining an even number”? two dice and thrown twice, we get totally 4 numbers. is it valid if only one number is even, or at least one of these 4 numbers is even or all 4 numbers must be even?

$${i}\:{also}\:{think}\:{that}\:{the}\:{question}\:{is}\:{not} \\ $$$${clear}.\:{what}\:{means}\:``{obtaining}\:{an} \\ $$$${even}\:{number}''?\:{two}\:{dice}\:{and}\:{thrown} \\ $$$${twice},\:{we}\:{get}\:{totally}\:\mathrm{4}\:{numbers}.\:{is} \\ $$$${it}\:{valid}\:{if}\:{only}\:{one}\:{number}\:{is}\:{even}, \\ $$$${or}\:{at}\:{least}\:{one}\:{of}\:{these}\:\mathrm{4}\:{numbers}\: \\ $$$${is}\:{even}\:{or}\:{all}\:\mathrm{4}\:{numbers}\:{must}\:{be}\: \\ $$$${even}? \\ $$

Commented by Frix last updated on 23/Mar/25

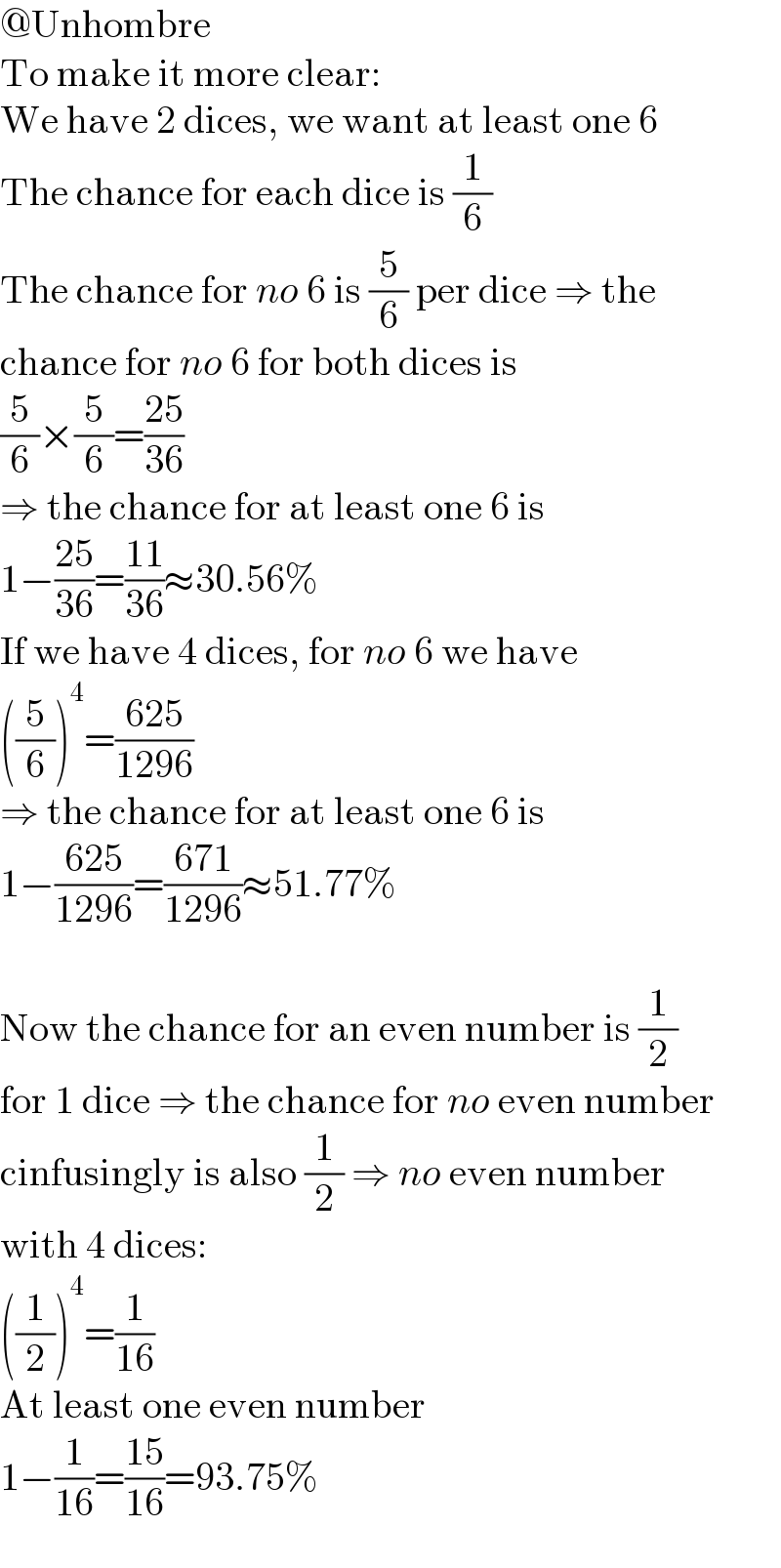
@Unhombre To make it more clear: We have 2 dices, we want at least one 6 The chance for each dice is (1/6) The chance for no 6 is (5/6) per dice ⇒ the chance for no 6 for both dices is (5/6)×(5/6)=((25)/(36)) ⇒ the chance for at least one 6 is 1−((25)/(36))=((11)/(36))≈30.56% If we have 4 dices, for no 6 we have ((5/6))^4 =((625)/(1296)) ⇒ the chance for at least one 6 is 1−((625)/(1296))=((671)/(1296))≈51.77% Now the chance for an even number is (1/2) for 1 dice ⇒ the chance for no even number cinfusingly is also (1/2) ⇒ no even number with 4 dices: ((1/2))^4 =(1/(16)) At least one even number 1−(1/(16))=((15)/(16))=93.75%

$$@\mathrm{Unhombre} \\ $$$$\mathrm{To}\:\mathrm{make}\:\mathrm{it}\:\mathrm{more}\:\mathrm{clear}: \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{2}\:\mathrm{dices},\:\mathrm{we}\:\mathrm{want}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{6} \\ $$$$\mathrm{The}\:\mathrm{chance}\:\mathrm{for}\:\mathrm{each}\:\mathrm{dice}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{The}\:\mathrm{chance}\:\mathrm{for}\:{no}\:\mathrm{6}\:\mathrm{is}\:\frac{\mathrm{5}}{\mathrm{6}}\:\mathrm{per}\:\mathrm{dice}\:\Rightarrow\:\mathrm{the} \\ $$$$\mathrm{chance}\:\mathrm{for}\:{no}\:\mathrm{6}\:\mathrm{for}\:\mathrm{both}\:\mathrm{dices}\:\mathrm{is} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{25}}{\mathrm{36}} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{chance}\:\mathrm{for}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{6}\:\mathrm{is} \\ $$$$\mathrm{1}−\frac{\mathrm{25}}{\mathrm{36}}=\frac{\mathrm{11}}{\mathrm{36}}\approx\mathrm{30}.\mathrm{56\%} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{have}\:\mathrm{4}\:\mathrm{dices},\:\mathrm{for}\:{no}\:\mathrm{6}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{4}} =\frac{\mathrm{625}}{\mathrm{1296}} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{chance}\:\mathrm{for}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{6}\:\mathrm{is} \\ $$$$\mathrm{1}−\frac{\mathrm{625}}{\mathrm{1296}}=\frac{\mathrm{671}}{\mathrm{1296}}\approx\mathrm{51}.\mathrm{77\%} \\ $$$$ \\ $$$$\mathrm{Now}\:\mathrm{the}\:\mathrm{chance}\:\mathrm{for}\:\mathrm{an}\:\mathrm{even}\:\mathrm{number}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{1}\:\mathrm{dice}\:\Rightarrow\:\mathrm{the}\:\mathrm{chance}\:\mathrm{for}\:{no}\:\mathrm{even}\:\mathrm{number} \\ $$$$\mathrm{cinfusingly}\:\mathrm{is}\:\mathrm{also}\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{no}\:\mathrm{even}\:\mathrm{number} \\ $$$$\mathrm{with}\:\mathrm{4}\:\mathrm{dices}: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{At}\:\mathrm{least}\:\mathrm{one}\:\mathrm{even}\:\mathrm{number} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}=\frac{\mathrm{15}}{\mathrm{16}}=\mathrm{93}.\mathrm{75\%} \\ $$

Commented by Tawa11 last updated on 23/Mar/25

If it is possible to do everything as a question. It will be fine. Find the probability of getting a sum of even numbers.

$$\mathrm{If}\:\mathrm{it}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{do}\:\mathrm{everything}\:\mathrm{as}\:\mathrm{a} \\ $$$$\mathrm{question}.\:\mathrm{It}\:\mathrm{will}\:\mathrm{be}\:\mathrm{fine}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{getting}\:\mathrm{a}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{even}\:\mathrm{numbers}. \\ $$

Commented by Tawa11 last updated on 23/Mar/25

If two fair dice is thrown twice, what is the probability of obtaining an even number. (That is, sum of the numbers is even). This is what I think.

$$ \\ $$If two fair dice is thrown twice, what is the probability of obtaining an even number. (That is, sum of the numbers is even). This is what I think.

Commented by mr W last updated on 24/Mar/25

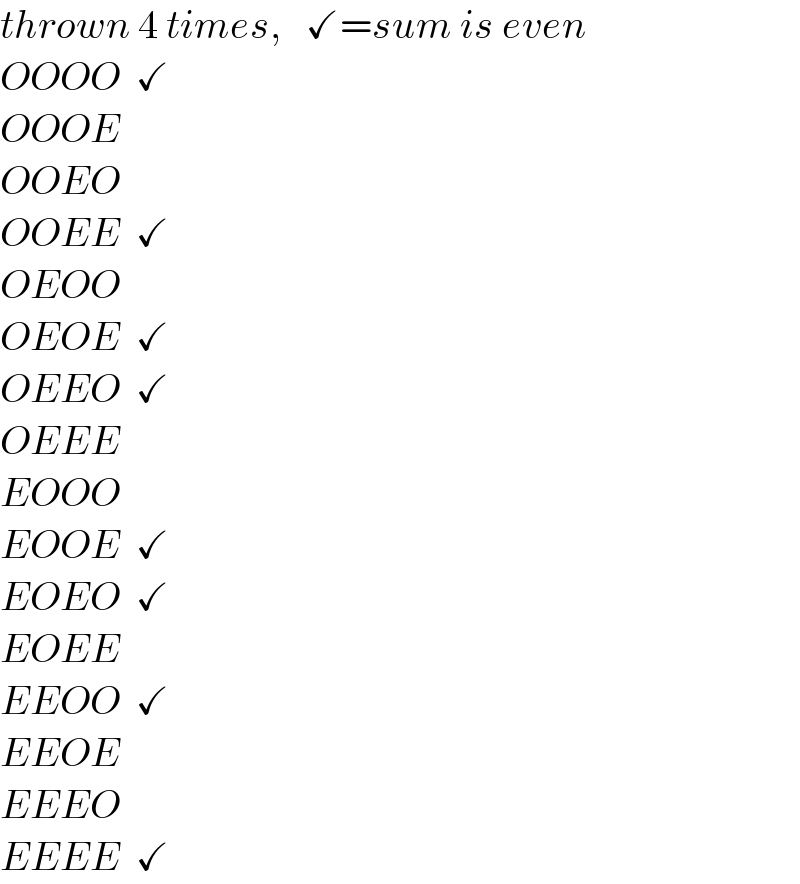
thrown 4 times, ✓=sum is even OOOO ✓ OOOE OOEO OOEE ✓ OEOO OEOE ✓ OEEO ✓ OEEE EOOO EOOE ✓ EOEO ✓ EOEE EEOO ✓ EEOE EEEO EEEE ✓

$${thrown}\:\mathrm{4}\:{times},\:\:\:\checkmark={sum}\:{is}\:{even} \\ $$$${OOOO}\:\:\checkmark \\ $$$${OOOE} \\ $$$${OOEO} \\ $$$${OOEE}\:\:\checkmark \\ $$$${OEOO} \\ $$$${OEOE}\:\:\checkmark \\ $$$${OEEO}\:\:\checkmark \\ $$$${OEEE} \\ $$$${EOOO} \\ $$$${EOOE}\:\:\checkmark \\ $$$${EOEO}\:\:\checkmark \\ $$$${EOEE} \\ $$$${EEOO}\:\:\checkmark \\ $$$${EEOE} \\ $$$${EEEO} \\ $$$${EEEE}\:\:\checkmark \\ $$

Commented by mr W last updated on 24/Mar/25

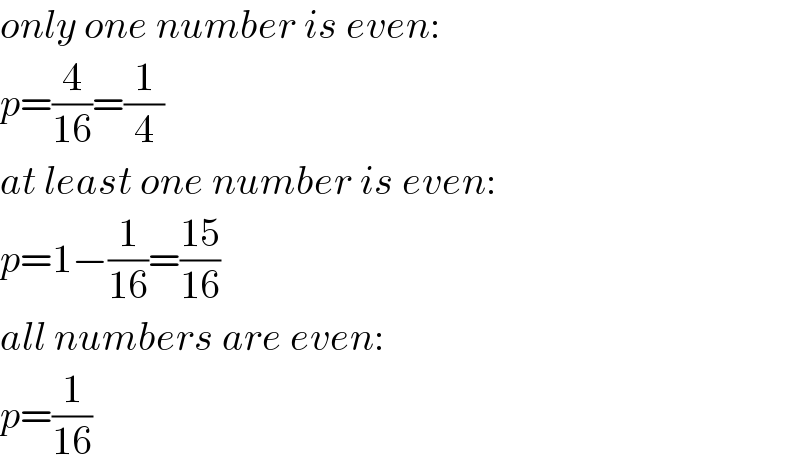
only one number is even: p=(4/(16))=(1/4) at least one number is even: p=1−(1/(16))=((15)/(16)) all numbers are even: p=(1/(16))

$${only}\:{one}\:{number}\:{is}\:{even}: \\ $$$${p}=\frac{\mathrm{4}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${at}\:{least}\:{one}\:{number}\:{is}\:{even}: \\ $$$${p}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}=\frac{\mathrm{15}}{\mathrm{16}} \\ $$$${all}\:{numbers}\:{are}\:{even}: \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$

Commented by Tawa11 last updated on 24/Mar/25

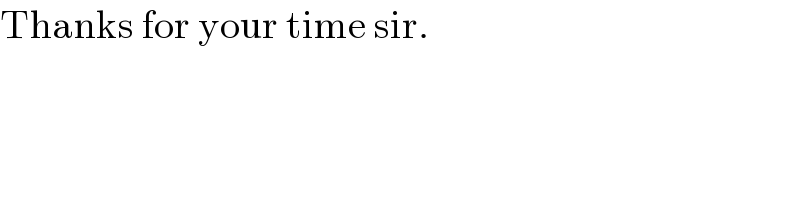
Thanks for your time sir.

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 24/Mar/25

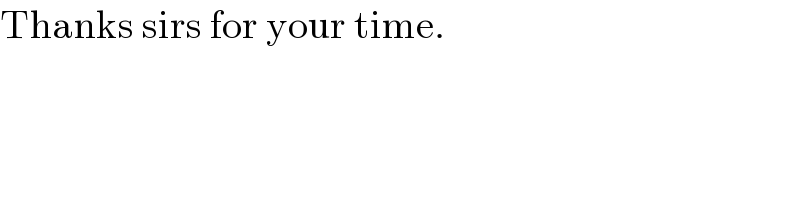
Thanks sirs for your time.

$$\mathrm{Thanks}\:\mathrm{sirs}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Commented by mr W last updated on 25/Mar/25

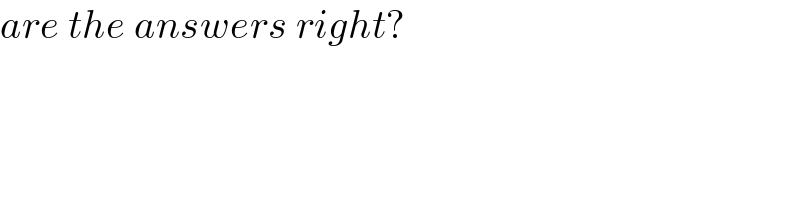
are the answers right?

$${are}\:{the}\:{answers}\:{right}? \\ $$

Commented by Tawa11 last updated on 25/Mar/25

I don′t know the answers sir. But you got the same answer as sir frix.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{answers}\:\mathrm{sir}. \\ $$$$\mathrm{But}\:\mathrm{you}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer} \\ $$$$\mathrm{as}\:\mathrm{sir}\:\mathrm{frix}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com