
Question Number 200353 by deleteduser12 last updated on 17/Nov/23
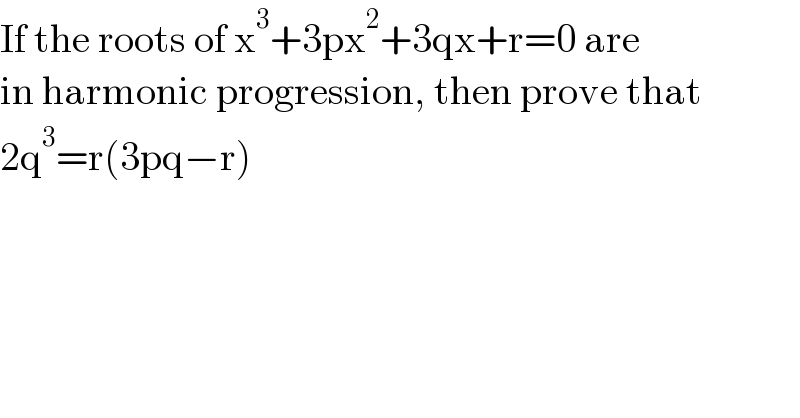
$$\mathrm{If}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}} +\mathrm{3px}^{\mathrm{2}} +\mathrm{3qx}+\mathrm{r}=\mathrm{0}\:\mathrm{are} \\ $$$$\mathrm{in}\:\mathrm{harmonic}\:\mathrm{progression},\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{2q}^{\mathrm{3}} =\mathrm{r}\left(\mathrm{3pq}−\mathrm{r}\right) \\ $$
Answered by jabarsing last updated on 18/Nov/23

$$ \\ $$To prove that the equation \(2q^3 = r(3pq - r)\) holds when the roots of \(x^3 + 3px^2 + 3qx + r = 0\) are in harmonic progression, we can start by assuming that the roots are \(a, \frac{1}{a},\) and \(-a - \frac{1}{a}\), where \(a \neq 0\). Using Vieta's formulas, we know that the sum of the roots is zero, so \(a + \frac{1}{a} - a - \frac{1}{a} = 0\), which is true. Now, let's find the value of \(q\) using the sum of the product of the roots taken two at a time. We have: \(a \cdot \frac{1}{a} + a \cdot \left(-a - \frac{1}{a}\right) + \frac{1}{a} \cdot \left(-a - \frac{1}{a}\right) = 3q\) Simplifying this expression, we get: \(1 - a^2 - 1 - \frac{1}{a^2} = 3q\) \(-a^2 - \frac{1}{a^2} = 3q\) Multiplying both sides by \(-1\), we have: \(a^2 + \frac{1}{a^2} = -3q\) Now, let's find the value of \(r\) using the product of the roots. We have: \(a \cdot \frac{1}{a} \cdot \left(-a - \frac{1}{a}\right) = -r\) Simplifying this expression, we get: \(-a - \frac{1}{a} = -r\) Multiplying both sides by \(-1\), we have: \(a + \frac{1}{a} = r\) Now, let's substitute the value of \(r\) in terms of \(a\) into the equation we found for \(q\): \(a^2 + \frac{1}{a^2} = -3q\) \(2q = -\left(a^2 + \frac{1}{a^2}\right)\) Squaring both sides, we get: \(4q^2 = \left(a^2 + \frac{1}{a^2}\right)^2\) Expanding the right side, we have: \(4q^2 = a^4 + 2 + \frac{1}{a^4}\) Now, let's multiply both sides by \(a^4\) to eliminate the fractions: \(4a^4q^2 = a^8 + 2a^4 + 1\) Rearranging the terms, we get: \(a^8 + 2a^4 - 4a^4q^2 + 1 = 0\) Now, notice that the equation \(x^3 + 3px^2 + 3qx + r = 0\) has roots \(a, \frac{1}{a},\) and \(-a - \frac{1}{a}\). Therefore, we can rewrite the equation as: \((x - a)\left(x - \frac{1}{a}\right)\left(x + a + \frac{1}{a}\right) = 0\) Expanding this equation, we get: \(x^3 + \left(a + \frac{1}{a}\right)x^2 + \left(-a - \frac{1}{a}\right)x - 1 = 0\) Comparing the coefficients of this equation with the original equation, we can see that: \(a + \frac{1}{a} = -3p\) and \(-a - \frac{1}{a} = r\) Substituting these values into the equation we obtained earlier, we have: \(a^8 + 2a^4 - 4a^4q^2 + 1 = 0\) \((-3p)^4 + 2(-3p)^2 - 4(-3p)^2q^2 + 1 = 0\) Simplifying this equation, we get: \(81p^4 + 18p^2 - 36p^2q^2 + 1 = 0\) Dividing both sides by \(9\), we have: \(9p^4 + 2p^2 - 4p^2q^2 + \frac{1}{9} = 0\) Now, notice that \(9p^4\) and \(\frac{1}{9}\) are perfect squares, so we can rewrite the equation as: \(\left
Commented by jabarsing last updated on 18/Nov/23

$$ \\ $$We can write the equation as follows: \((x - a)(x - \frac{1}{a})(x + a + \frac{1}{a}) = 0\) By multiplying this expression, we get: \((x^2 - ax - \frac{1}{a}x + \frac{1}{a^2})(x + a + \frac{1}{a}) = 0\) Simplifying this expression, we obtain: \(x^3 + (a + \frac{1}{a})x^2 + (a^2 + 1 + \frac{1}{a^2})x + (a + \frac{1}{a}) = 0\) By comparing this expression with the original equation, we can expand the following relationships: \(a + \frac{1}{a} = -3p\) \(a^2 + 1 + \frac{1}{a^2} = -3q\) \(a + \frac{1}{a} = -r\) Now, by adding the first and third equations, we get: \(2(a + \frac{1}{a}) = -3p - r\) By substituting the value of \(r\) from the fourth equation, we get: \(2q = -3p - r\) By multiplying both sides of this equation by \(2q\), we get: \(4q^2 = -6pq - 2qr\) By adding this equation to the previous equation we obtained for \(q\), we get: \(4q^2 + 2q = -6pq - 2qr - 3pq + r(3pq - r)\) Simplifying this expression, we get: \(2q(2q + 1) = r(3pq - r)\) And by dividing both sides of this equation by 2, we get: \(q^2 + q = \frac{r(3pq - r)}{2}\) Finally, by multiplying both sides of this equation by 2, we get: \(2q^3 = r(3pq - r)\) Thus, assuming that the roots of the equation are in a harmonic sequence, we have arrived at the equation \(2q^3 = r(3pq - r)\).
Answered by ajfour last updated on 17/Nov/23
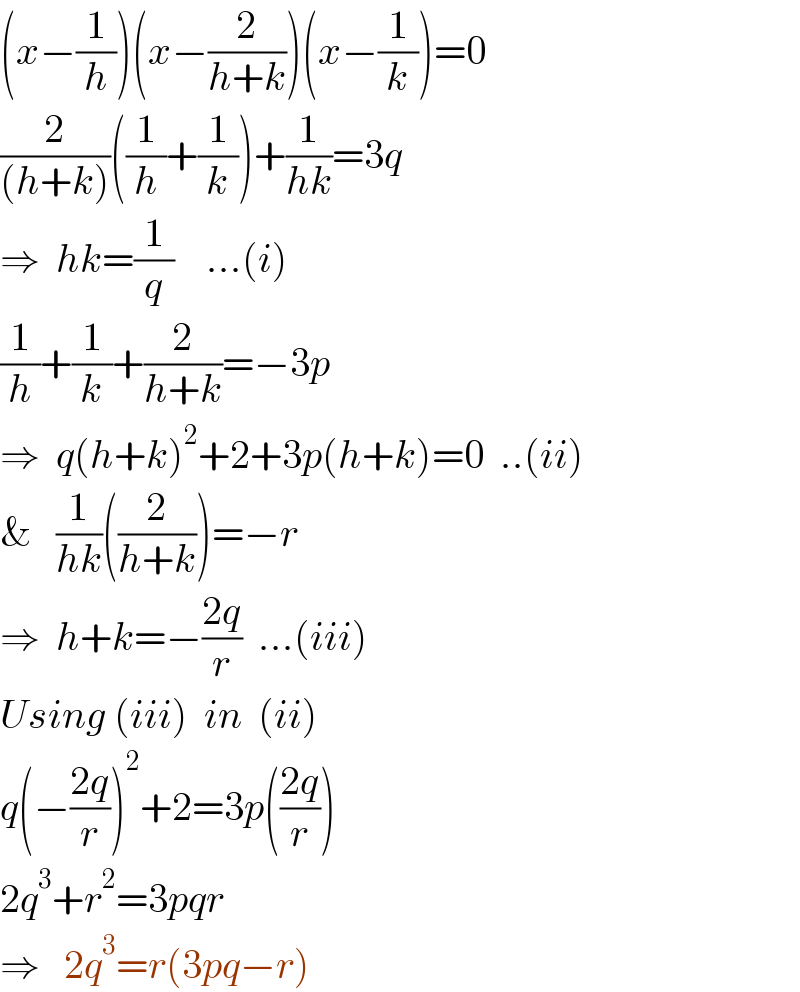
$$\left({x}−\frac{\mathrm{1}}{{h}}\right)\left({x}−\frac{\mathrm{2}}{{h}+{k}}\right)\left({x}−\frac{\mathrm{1}}{{k}}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\left({h}+{k}\right)}\left(\frac{\mathrm{1}}{{h}}+\frac{\mathrm{1}}{{k}}\right)+\frac{\mathrm{1}}{{hk}}=\mathrm{3}{q} \\ $$$$\Rightarrow\:\:{hk}=\frac{\mathrm{1}}{{q}}\:\:\:\:...\left({i}\right) \\ $$$$\frac{\mathrm{1}}{{h}}+\frac{\mathrm{1}}{{k}}+\frac{\mathrm{2}}{{h}+{k}}=−\mathrm{3}{p} \\ $$$$\Rightarrow\:\:{q}\left({h}+{k}\right)^{\mathrm{2}} +\mathrm{2}+\mathrm{3}{p}\left({h}+{k}\right)=\mathrm{0}\:\:..\left({ii}\right) \\ $$$$\&\:\:\:\frac{\mathrm{1}}{{hk}}\left(\frac{\mathrm{2}}{{h}+{k}}\right)=−{r} \\ $$$$\Rightarrow\:\:{h}+{k}=−\frac{\mathrm{2}{q}}{{r}}\:\:...\left({iii}\right) \\ $$$${Using}\:\left({iii}\right)\:\:{in}\:\:\left({ii}\right) \\ $$$${q}\left(−\frac{\mathrm{2}{q}}{{r}}\right)^{\mathrm{2}} +\mathrm{2}=\mathrm{3}{p}\left(\frac{\mathrm{2}{q}}{{r}}\right) \\ $$$$\mathrm{2}{q}^{\mathrm{3}} +{r}^{\mathrm{2}} =\mathrm{3}{pqr} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{q}^{\mathrm{3}} ={r}\left(\mathrm{3}{pq}−{r}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 17/Nov/23
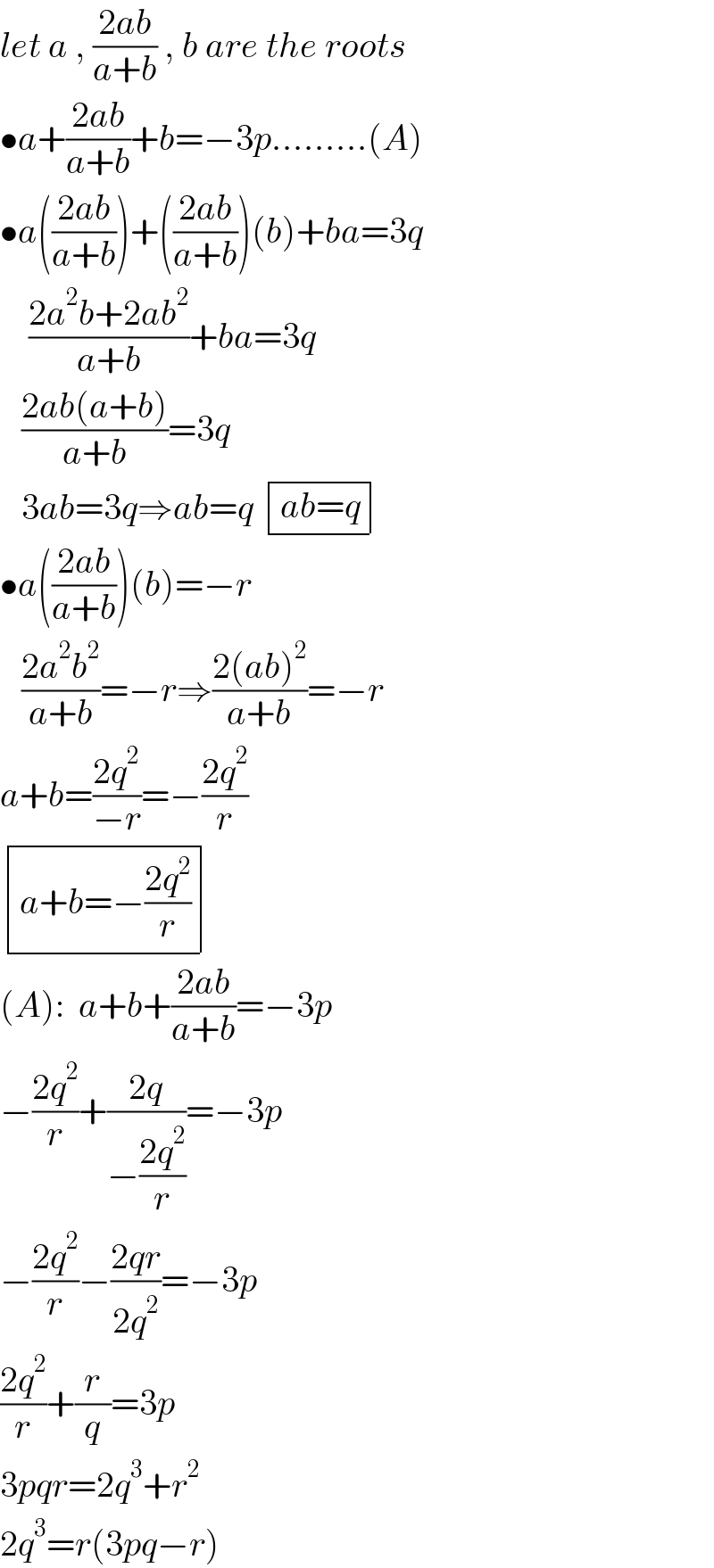
$${let}\:{a}\:,\:\frac{\mathrm{2}{ab}}{{a}+{b}}\:,\:{b}\:{are}\:{the}\:{roots} \\ $$$$\bullet{a}+\frac{\mathrm{2}{ab}}{{a}+{b}}+{b}=−\mathrm{3}{p}.........\left({A}\right) \\ $$$$\bullet{a}\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)+\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)\left({b}\right)+{ba}=\mathrm{3}{q} \\ $$$$\:\:\:\:\frac{\mathrm{2}{a}^{\mathrm{2}} {b}+\mathrm{2}{ab}^{\mathrm{2}} }{{a}+{b}}+{ba}=\mathrm{3}{q} \\ $$$$\:\:\:\frac{\mathrm{2}{ab}\left({a}+{b}\right)}{{a}+{b}}=\mathrm{3}{q} \\ $$$$\:\:\:\mathrm{3}{ab}=\mathrm{3}{q}\Rightarrow{ab}={q}\:\begin{array}{|c|}{{ab}={q}}\\\hline\end{array} \\ $$$$\bullet{a}\left(\frac{\mathrm{2}{ab}}{{a}+{b}}\right)\left({b}\right)=−{r} \\ $$$$\:\:\:\frac{\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}+{b}}=−{r}\Rightarrow\frac{\mathrm{2}\left({ab}\right)^{\mathrm{2}} }{{a}+{b}}=−{r} \\ $$$${a}+{b}=\frac{\mathrm{2}{q}^{\mathrm{2}} }{−{r}}=−\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}} \\ $$$$\begin{array}{|c|}{{a}+{b}=−\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}}}\\\hline\end{array} \\ $$$$\left({A}\right):\:\:{a}+{b}+\frac{\mathrm{2}{ab}}{{a}+{b}}=−\mathrm{3}{p} \\ $$$$−\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}}+\frac{\mathrm{2}{q}}{−\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}}}=−\mathrm{3}{p} \\ $$$$−\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}}−\frac{\mathrm{2}{qr}}{\mathrm{2}{q}^{\mathrm{2}} }=−\mathrm{3}{p} \\ $$$$\frac{\mathrm{2}{q}^{\mathrm{2}} }{{r}}+\frac{{r}}{{q}}=\mathrm{3}{p} \\ $$$$\mathrm{3}{pqr}=\mathrm{2}{q}^{\mathrm{3}} +{r}^{\mathrm{2}} \\ $$$$\mathrm{2}{q}^{\mathrm{3}} ={r}\left(\mathrm{3}{pq}−{r}\right) \\ $$
