
Question Number 210362 by MATHEMATICSAM last updated on 10/Sep/24
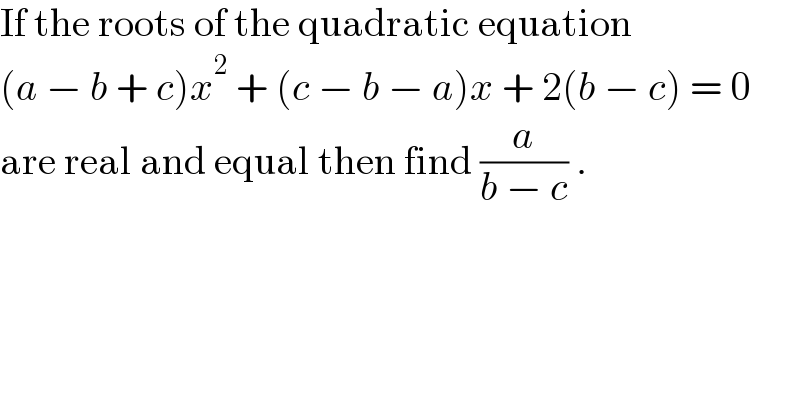
$$\mathrm{If}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$$\left({a}\:−\:{b}\:+\:{c}\right){x}^{\mathrm{2}} \:+\:\left({c}\:−\:{b}\:−\:{a}\right){x}\:+\:\mathrm{2}\left({b}\:−\:{c}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{are}\:\mathrm{real}\:\mathrm{and}\:\mathrm{equal}\:\mathrm{then}\:\mathrm{find}\:\frac{{a}}{{b}\:−\:{c}}\:. \\ $$
Commented by som(math1967) last updated on 08/Aug/24
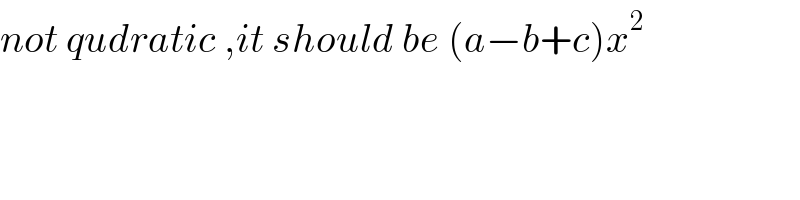
$${not}\:{qudratic}\:,{it}\:{should}\:{be}\:\left({a}−{b}+{c}\right){x}^{\mathrm{2}} \\ $$
Commented by MATHEMATICSAM last updated on 10/Sep/24

$$\mathrm{oh}\:\mathrm{yes} \\ $$
Answered by som(math1967) last updated on 11/Sep/24
![let (a−b+c)=p ,(c−b−a)=q 2(b−c)=r ∴p+q+r=a−b+c+c−b−a+2b−2c =0 equation⇒px^2 +qx+r=0 roots are real and equal ∴q^2 =4pr ⇒(p+r)^2 =4pr [∵p+q+r=0] ⇒(p−r)^2 =0 ⇒p−r=0⇒p=r ⇒ a−b+c=2(b−c) ⇒a+c+2c=2b+b ⇒a=3(b−c) ∴ (a/(b−c))=3](Q211491.png)
$${let}\:\left({a}−{b}+{c}\right)={p}\:,\left({c}−{b}−{a}\right)={q} \\ $$$$\mathrm{2}\left({b}−{c}\right)={r} \\ $$$$\therefore{p}+{q}+{r}={a}−{b}+{c}+{c}−{b}−{a}+\mathrm{2}{b}−\mathrm{2}{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$$$\:{equation}\Rightarrow{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0} \\ $$$$\:{roots}\:{are}\:{real}\:{and}\:{equal} \\ $$$$\:\:\therefore{q}^{\mathrm{2}} =\mathrm{4}{pr} \\ $$$$\Rightarrow\left({p}+{r}\right)^{\mathrm{2}} =\mathrm{4}{pr}\:\left[\because{p}+{q}+{r}=\mathrm{0}\right] \\ $$$$\Rightarrow\left({p}−{r}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}−{r}=\mathrm{0}\Rightarrow{p}={r} \\ $$$$\Rightarrow\:{a}−{b}+{c}=\mathrm{2}\left({b}−{c}\right) \\ $$$$\Rightarrow{a}+{c}+\mathrm{2}{c}=\mathrm{2}{b}+{b} \\ $$$$\Rightarrow{a}=\mathrm{3}\left({b}−{c}\right) \\ $$$$\therefore\:\frac{{a}}{{b}−{c}}=\mathrm{3} \\ $$
