
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 210832 by BaliramKumar last updated on 19/Aug/24

$$ \\ $$If the probability of A solving a question is 1/2 and the probability of B solving the question is 2/3 then the probability of the question being solved is
Commented by mr W last updated on 20/Aug/24
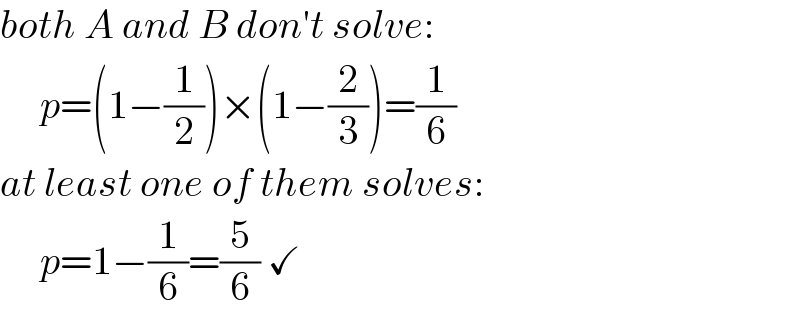
$${both}\:{A}\:{and}\:{B}\:{don}'{t}\:{solve}:\: \\ $$$$\:\:\:\:\:{p}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)×\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${at}\:{least}\:{one}\:{of}\:{them}\:{solves}: \\ $$$$\:\:\:\:\:{p}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{6}}\:\checkmark \\ $$
Answered by Ghisom last updated on 20/Aug/24
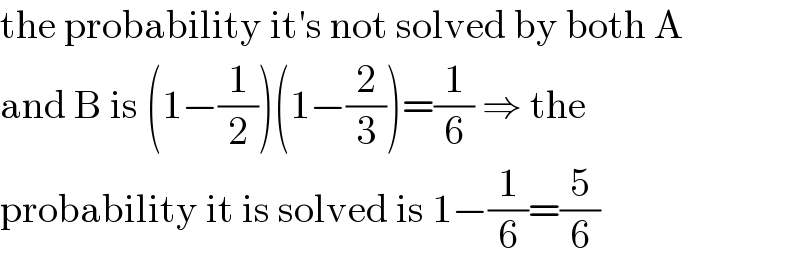
$$\mathrm{the}\:\mathrm{probability}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{both}\:\mathrm{A} \\ $$$$\mathrm{and}\:\mathrm{B}\:\mathrm{is}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\:\mathrm{the} \\ $$$$\mathrm{probability}\:\mathrm{it}\:\mathrm{is}\:\mathrm{solved}\:\mathrm{is}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Answered by BHOOPENDRA last updated on 20/Aug/24
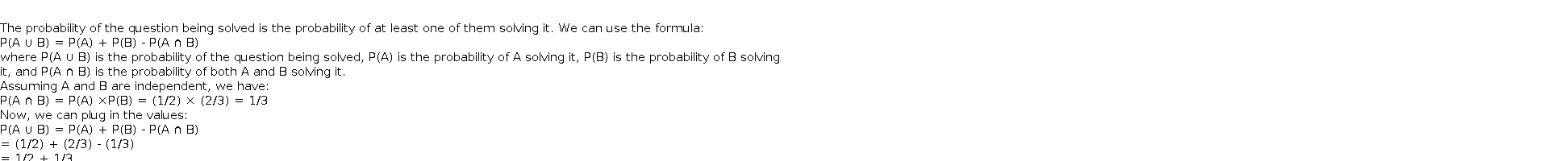
$$ \\ $$The probability of the question being solved is the probability of at least one of them solving it. We can use the formula: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) where P(A ∪ B) is the probability of the question being solved, P(A) is the probability of A solving it, P(B) is the probability of B solving it, and P(A ∩ B) is the probability of both A and B solving it. Assuming A and B are independent, we have: P(A ∩ B) = P(A) ×P(B) = (1/2) × (2/3) = 1/3 Now, we can plug in the values: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = (1/2) + (2/3) - (1/3) = 1/2 + 1/3 = 5/6 So, the probability of the question being solved is 5/6. To find the probability of the question being unsolved, we can use the complement rule: P(unsolved) = 1 - P(solved) We already found the probability of the question being solved: P(solved) = 5/6 So, the probability of the question being unsolved is: P(unsolved) = 1 - 5/6 = 1/6 Therefore, the probability of the question being unsolved is 1/6.
