
Question Number 105345 by bemath last updated on 28/Jul/20
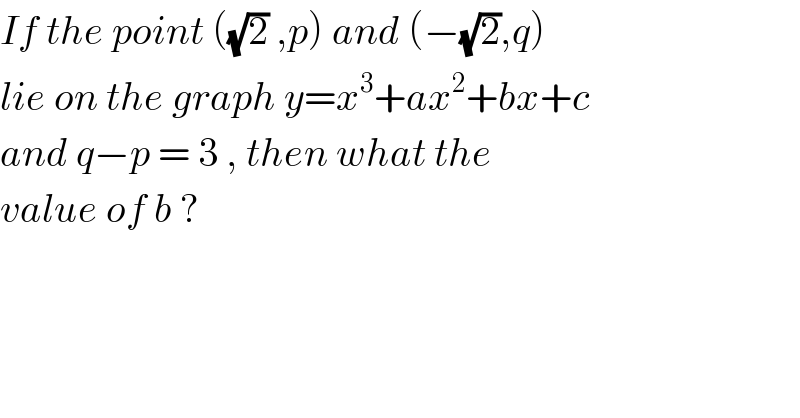
$${If}\:{the}\:{point}\:\left(\sqrt{\mathrm{2}}\:,{p}\right)\:{and}\:\left(−\sqrt{\mathrm{2}},{q}\right) \\ $$$${lie}\:{on}\:{the}\:{graph}\:{y}={x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${and}\:{q}−{p}\:=\:\mathrm{3}\:,\:{then}\:{what}\:{the} \\ $$$${value}\:{of}\:{b}\:?\: \\ $$
Answered by ajfour last updated on 28/Jul/20
![p=2(√2)+2a+b(√2)+c q=−2(√2)+2a−b(√2)+c subtracting −3=2(√2)(b+2) ⇒ b=−2−((3(√2))/4) b = −[2+(3/4)((√2))] .](Q105357.png)
$${p}=\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}{a}+{b}\sqrt{\mathrm{2}}+{c} \\ $$$${q}=−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}{a}−{b}\sqrt{\mathrm{2}}+{c} \\ $$$${subtracting} \\ $$$$−\mathrm{3}=\mathrm{2}\sqrt{\mathrm{2}}\left({b}+\mathrm{2}\right)\:\:\:\Rightarrow\:\:{b}=−\mathrm{2}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\:{b}\:=\:−\left[\mathrm{2}+\frac{\mathrm{3}}{\mathrm{4}}\left(\sqrt{\mathrm{2}}\right)\right]\:. \\ $$
Commented by bemath last updated on 28/Jul/20

$${cooll}... \\ $$
