Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 206993 by necx122 last updated on 03/May/24

If the nth term of a sequence is given by ((n^2 −2n)/4) ,what is the sum of n terms of the sequence?

$${If}\:{the}\:{nth}\:{term}\:{of}\:{a}\:{sequence}\:{is} \\ $$$${given}\:{by}\:\frac{{n}^{\mathrm{2}} −\mathrm{2}{n}}{\mathrm{4}}\:,{what}\:{is}\:{the}\:{sum}\:{of}\:{n} \\ $$$${terms}\:{of}\:{the}\:{sequence}? \\ $$

Answered by Rasheed.Sindhi last updated on 03/May/24

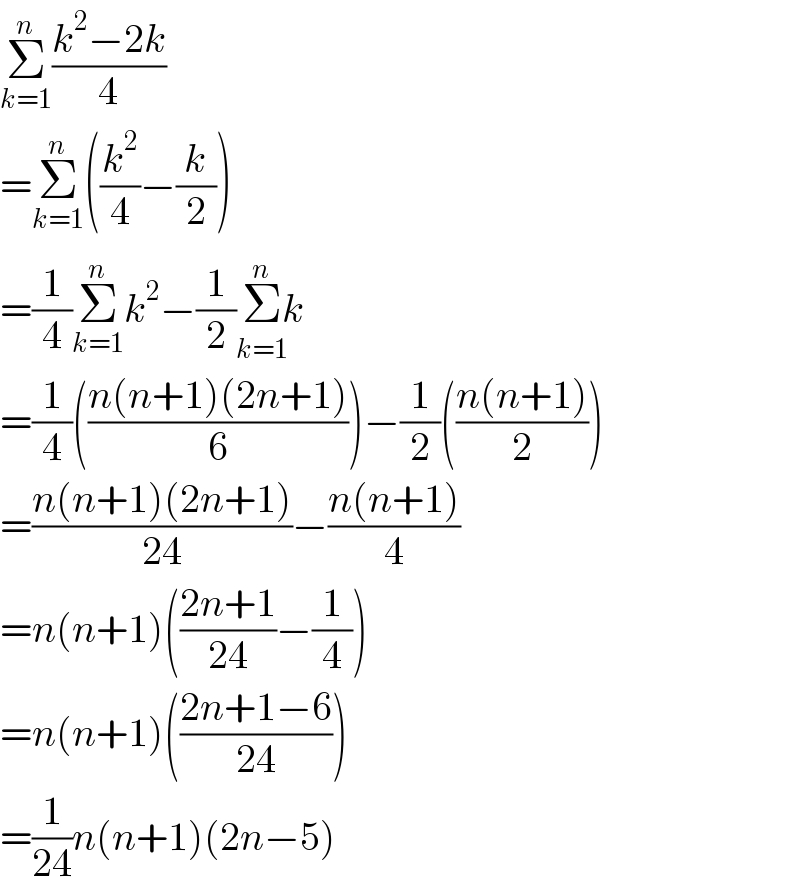
Σ_(k=1) ^n ((k^2 −2k)/4) =Σ_(k=1) ^n ((k^2 /4)−(k/2)) =(1/4)Σ_(k=1) ^n k^2 −(1/2)Σ_(k=1) ^(n) k =(1/4)(((n(n+1)(2n+1))/6))−(1/2)(((n(n+1))/2)) =((n(n+1)(2n+1))/(24))−((n(n+1))/4) =n(n+1)(((2n+1)/(24))−(1/4)) =n(n+1)(((2n+1−6)/(24))) =(1/(24))n(n+1)(2n−5)

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} −\mathrm{2}{k}}{\mathrm{4}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\Sigma}}{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{24}}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}} \\ $$$$={n}\left({n}+\mathrm{1}\right)\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$={n}\left({n}+\mathrm{1}\right)\left(\frac{\mathrm{2}{n}+\mathrm{1}−\mathrm{6}}{\mathrm{24}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{5}\right) \\ $$

Commented by necx122 last updated on 04/May/24

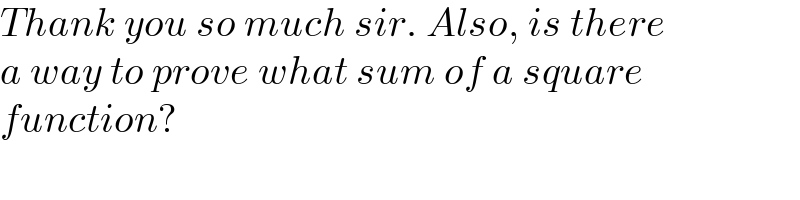
Thank you so much sir. Also, is there a way to prove what sum of a square function?

$${Thank}\:{you}\:{so}\:{much}\:{sir}.\:{Also},\:{is}\:{there} \\ $$$${a}\:{way}\:{to}\:{prove}\:{what}\:{sum}\:{of}\:{a}\:{square} \\ $$$${function}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com