
Question Number 18758 by 786786AM last updated on 29/Jul/17
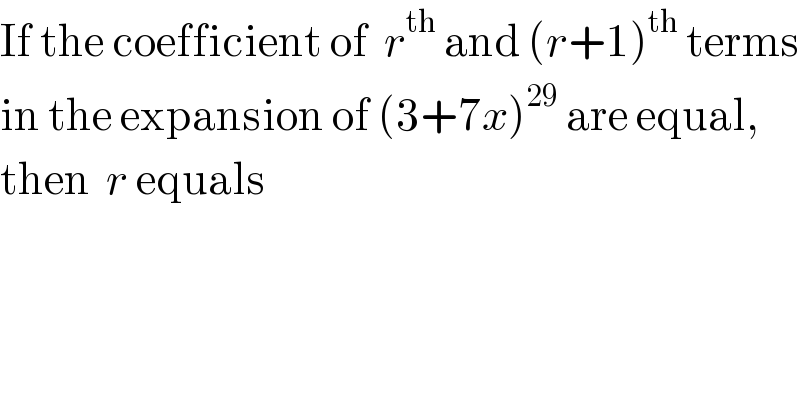
$$\mathrm{If}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\:{r}^{\mathrm{th}} \:\mathrm{and}\:\left({r}+\mathrm{1}\right)^{\mathrm{th}} \:\mathrm{terms} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{3}+\mathrm{7}{x}\right)^{\mathrm{29}} \:\mathrm{are}\:\mathrm{equal}, \\ $$$$\mathrm{then}\:\:{r}\:\mathrm{equals} \\ $$
Answered by Tinkutara last updated on 29/Jul/17
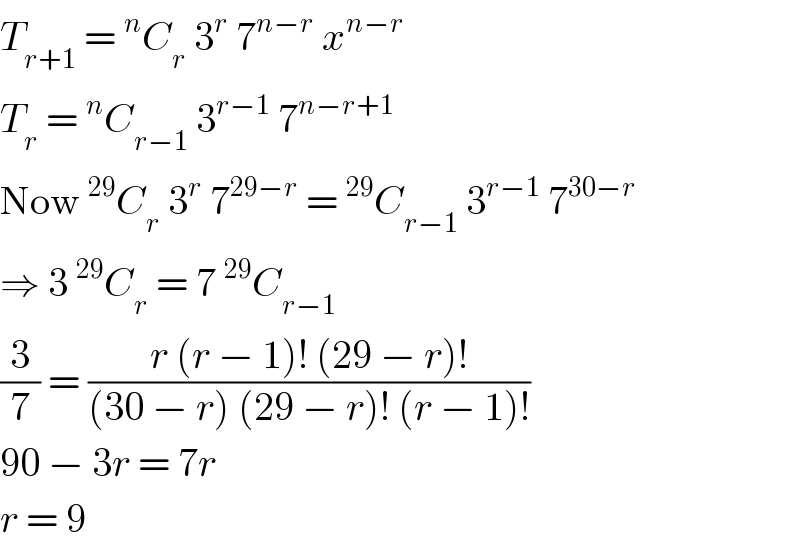
$${T}_{{r}+\mathrm{1}} \:=\:^{{n}} {C}_{{r}} \:\mathrm{3}^{{r}} \:\mathrm{7}^{{n}−{r}} \:{x}^{{n}−{r}} \\ $$$${T}_{{r}} \:=\:^{{n}} {C}_{{r}−\mathrm{1}} \:\mathrm{3}^{{r}−\mathrm{1}} \:\mathrm{7}^{{n}−{r}+\mathrm{1}} \\ $$$$\mathrm{Now}\:^{\mathrm{29}} {C}_{{r}} \:\mathrm{3}^{{r}} \:\mathrm{7}^{\mathrm{29}−{r}} \:=\:^{\mathrm{29}} {C}_{{r}−\mathrm{1}} \:\mathrm{3}^{{r}−\mathrm{1}} \:\mathrm{7}^{\mathrm{30}−{r}} \\ $$$$\Rightarrow\:\mathrm{3}\:^{\mathrm{29}} {C}_{{r}} \:=\:\mathrm{7}\:^{\mathrm{29}} {C}_{{r}−\mathrm{1}} \\ $$$$\frac{\mathrm{3}}{\mathrm{7}}\:=\:\frac{{r}\:\left({r}\:−\:\mathrm{1}\right)!\:\left(\mathrm{29}\:−\:{r}\right)!}{\left(\mathrm{30}\:−\:{r}\right)\:\left(\mathrm{29}\:−\:{r}\right)!\:\left({r}\:−\:\mathrm{1}\right)!} \\ $$$$\mathrm{90}\:−\:\mathrm{3}{r}\:=\:\mathrm{7}{r} \\ $$$${r}\:=\:\mathrm{9} \\ $$
