Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 206421 by MATHEMATICSAM last updated on 13/Apr/24

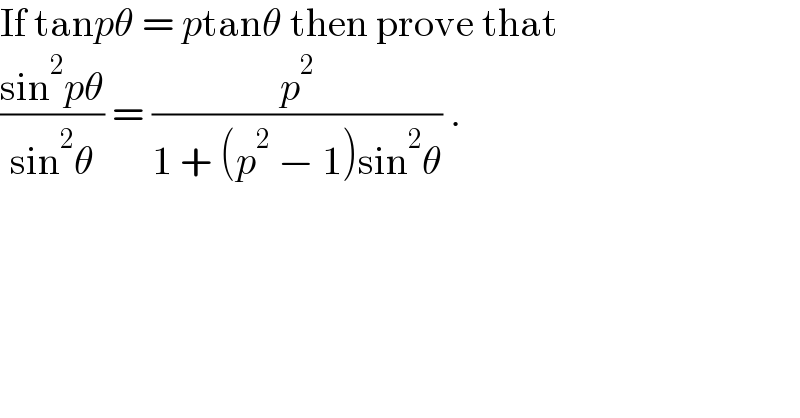
If tanpθ = ptanθ then prove that ((sin^2 pθ)/(sin^2 θ)) = (p^2 /(1 + (p^2 − 1)sin^2 θ)) .

$$\mathrm{If}\:\mathrm{tan}{p}\theta\:=\:{p}\mathrm{tan}\theta\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} {p}\theta}{\mathrm{sin}^{\mathrm{2}} \theta}\:=\:\frac{{p}^{\mathrm{2}} }{\mathrm{1}\:+\:\left({p}^{\mathrm{2}} \:−\:\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \theta}\:.\: \\ $$

Answered by Frix last updated on 13/Apr/24

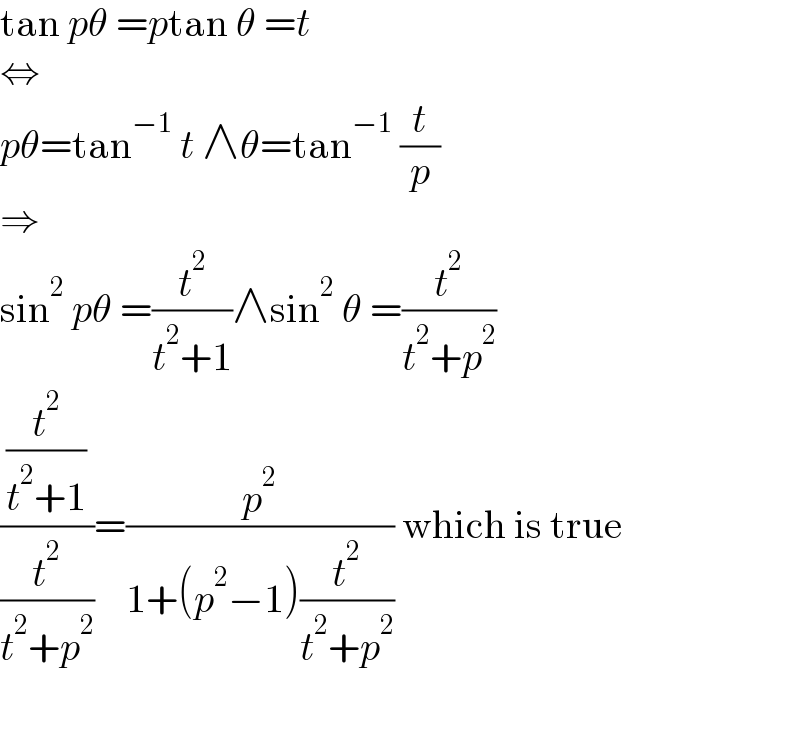
tan pθ =ptan θ =t ⇔ pθ=tan^(−1) t ∧θ=tan^(−1) (t/p) ⇒ sin^2 pθ =(t^2 /(t^2 +1))∧sin^2 θ =(t^2 /(t^2 +p^2 )) ((t^2 /(t^2 +1))/(t^2 /(t^2 +p^2 )))=(p^2 /(1+(p^2 −1)(t^2 /(t^2 +p^2 )))) which is true

$$\mathrm{tan}\:{p}\theta\:={p}\mathrm{tan}\:\theta\:={t} \\ $$$$\Leftrightarrow \\ $$$${p}\theta=\mathrm{tan}^{−\mathrm{1}} \:{t}\:\wedge\theta=\mathrm{tan}^{−\mathrm{1}} \:\frac{{t}}{{p}} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{p}\theta\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}\wedge\mathrm{sin}^{\mathrm{2}} \:\theta\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{p}^{\mathrm{2}} } \\ $$$$\frac{\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}}{\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{p}^{\mathrm{2}} }}=\frac{{p}^{\mathrm{2}} }{\mathrm{1}+\left({p}^{\mathrm{2}} −\mathrm{1}\right)\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{p}^{\mathrm{2}} }}\:\mathrm{which}\:\mathrm{is}\:\mathrm{true} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com