Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 16681 by rish@bh last updated on 25/Jun/17

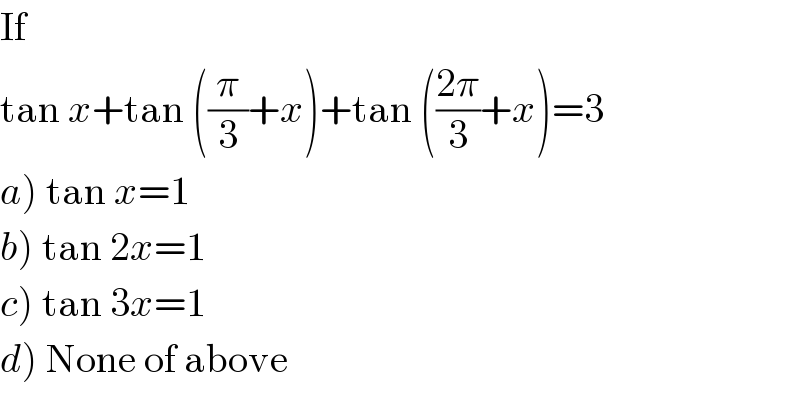
If tan x+tan ((π/3)+x)+tan (((2π)/3)+x)=3 a) tan x=1 b) tan 2x=1 c) tan 3x=1 d) None of above

$$\mathrm{If} \\ $$$$\mathrm{tan}\:{x}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+{x}\right)+\mathrm{tan}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+{x}\right)=\mathrm{3} \\ $$$$\left.{a}\right)\:\mathrm{tan}\:{x}=\mathrm{1} \\ $$$$\left.{b}\right)\:\mathrm{tan}\:\mathrm{2}{x}=\mathrm{1} \\ $$$$\left.{c}\right)\:\mathrm{tan}\:\mathrm{3}{x}=\mathrm{1} \\ $$$$\left.{d}\right)\:\mathrm{None}\:\mathrm{of}\:\mathrm{above} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/Jun/17

(((√3)+tgx)/(1−(√3)tgx))+((−(√3)+tgx)/(1+(√3)tgx))=3−tgx⇒ (((√3)+3tgx+tgx+(√3)tg^2 x−(√3)+tgx+3tgx−(√3)tg^2 x)/(1−3tg^2 x))=3−tgx ⇒((8tgx)/(1−3tg^2 x))=3−tgx⇒8tgx=3−tgx−9tg^2 x+3tg^3 x ⇒tg^3 x−3tg^2 x−3tgx+1=0 ⇒(tgx+1)(tg^2 x−4tgx+1)=0 ⇒tgx=−1,tgx=((4±(√(16−4)))/2)=2±(√3) .■ tgx=−1⇒tg2x=∞,tg3x=1 tgx=2−(√3)⇒x= { ((π/(12))),((tg2x=((√3)/3),tg3x=1)) :} tgx=2+(√3)⇒x= { (((5π)/(12))),((tg2x=−((√3)/3),tg3x=1)) :} so in all cases we have: tg3x=1⇒answer(c). way:2 x+(x+(π/3))+(x+((2π)/3))=π+3x ⇒tgx+tg(x+(π/3))+tg(x+((2π)/3))=tgx.tg(x+(π/3))tg(x+((2π)/3)) tg(x+((2π)/3))=−tg(π−(((2π)/3)+x))=−tg((π/3)−x)= =tg(x−(π/3)) tg3x=tgx.tg(x+(π/3))tg(x−(π/3)) ⇒3tg3x=3⇒tg3x=1 ⇒answer (c).

$$\frac{\sqrt{\mathrm{3}}+{tgx}}{\mathrm{1}−\sqrt{\mathrm{3}}{tgx}}+\frac{−\sqrt{\mathrm{3}}+{tgx}}{\mathrm{1}+\sqrt{\mathrm{3}}{tgx}}=\mathrm{3}−{tgx}\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{3}}+\mathrm{3}{tgx}+{tgx}+\sqrt{\mathrm{3}}{tg}^{\mathrm{2}} {x}−\sqrt{\mathrm{3}}+{tgx}+\mathrm{3}{tgx}−\sqrt{\mathrm{3}}{tg}^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} {x}}=\mathrm{3}−{tgx} \\ $$$$\Rightarrow\frac{\mathrm{8}{tgx}}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} {x}}=\mathrm{3}−{tgx}\Rightarrow\mathrm{8}{tgx}=\mathrm{3}−{tgx}−\mathrm{9}{tg}^{\mathrm{2}} {x}+\mathrm{3}{tg}^{\mathrm{3}} {x} \\ $$$$\Rightarrow{tg}^{\mathrm{3}} {x}−\mathrm{3}{tg}^{\mathrm{2}} {x}−\mathrm{3}{tgx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({tgx}+\mathrm{1}\right)\left({tg}^{\mathrm{2}} {x}−\mathrm{4}{tgx}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{tgx}=−\mathrm{1},{tgx}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}}\:.\blacksquare \\ $$$${tgx}=−\mathrm{1}\Rightarrow{tg}\mathrm{2}{x}=\infty,{tg}\mathrm{3}{x}=\mathrm{1} \\ $$$${tgx}=\mathrm{2}−\sqrt{\mathrm{3}}\Rightarrow{x}=\begin{cases}{\frac{\pi}{\mathrm{12}}}\\{{tg}\mathrm{2}{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},{tg}\mathrm{3}{x}=\mathrm{1}}\end{cases} \\ $$$${tgx}=\mathrm{2}+\sqrt{\mathrm{3}}\Rightarrow{x}=\begin{cases}{\frac{\mathrm{5}\pi}{\mathrm{12}}}\\{{tg}\mathrm{2}{x}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},{tg}\mathrm{3}{x}=\mathrm{1}}\end{cases} \\ $$$${so}\:{in}\:{all}\:{cases}\:{we}\:{have}:\:{tg}\mathrm{3}{x}=\mathrm{1}\Rightarrow{answer}\left({c}\right). \\ $$$${way}:\mathrm{2} \\ $$$${x}+\left({x}+\frac{\pi}{\mathrm{3}}\right)+\left({x}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=\pi+\mathrm{3}{x} \\ $$$$\Rightarrow{tgx}+{tg}\left({x}+\frac{\pi}{\mathrm{3}}\right)+{tg}\left({x}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)={tgx}.{tg}\left({x}+\frac{\pi}{\mathrm{3}}\right){tg}\left({x}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$${tg}\left({x}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=−{tg}\left(\pi−\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+{x}\right)\right)=−{tg}\left(\frac{\pi}{\mathrm{3}}−{x}\right)= \\ $$$$={tg}\left({x}−\frac{\pi}{\mathrm{3}}\right) \\ $$$${tg}\mathrm{3}{x}={tgx}.{tg}\left({x}+\frac{\pi}{\mathrm{3}}\right){tg}\left({x}−\frac{\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow\mathrm{3}{tg}\mathrm{3}{x}=\mathrm{3}\Rightarrow{tg}\mathrm{3}{x}=\mathrm{1}\:\Rightarrow{answer}\:\left({c}\right). \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com