Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 189468 by cortano12 last updated on 17/Mar/23

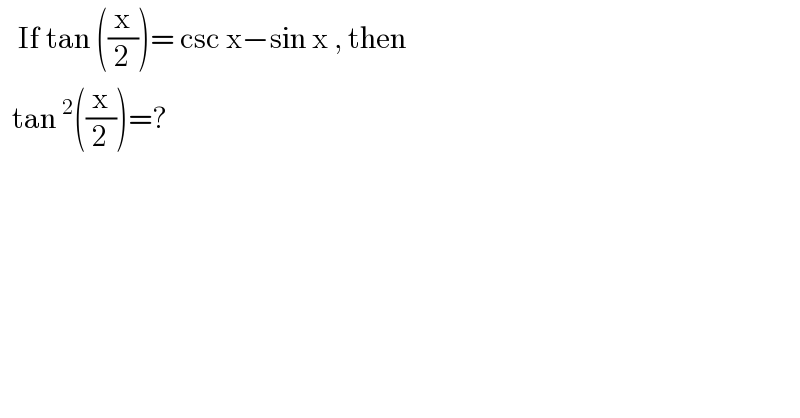
If tan ((x/2))= csc x−sin x , then tan^2 ((x/2))=?

$$\:\:\:\mathrm{If}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\:\mathrm{csc}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\:,\:\mathrm{then} \\ $$$$\:\:\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)=? \\ $$

Commented by mehdee42 last updated on 17/Mar/23

the given relation is wrong. tan((x/2))=cscx−cotx

$${the}\:{given}\:{relation}\:{is}\:{wrong}. \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={cscx}−{cotx} \\ $$

Commented by cortano12 last updated on 17/Mar/23

why wrong?

$$\mathrm{why}\:\mathrm{wrong}? \\ $$

Commented by Frix last updated on 17/Mar/23

Why do you think it′s a relation?

$$\mathrm{Why}\:\mathrm{do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{relation}? \\ $$

Commented by mehdee42 last updated on 17/Mar/23

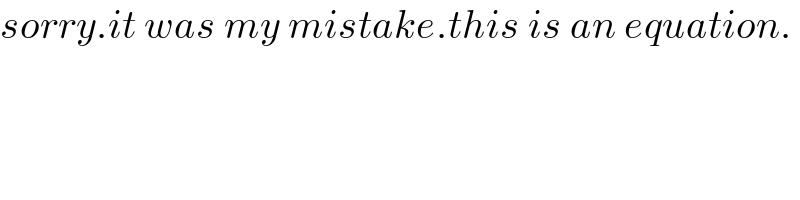
sorry.it was my mistake.this is an equation.

$${sorry}.{it}\:{was}\:{my}\:{mistake}.{this}\:{is}\:{an}\:{equation}.\: \\ $$

Answered by horsebrand11 last updated on 17/Mar/23

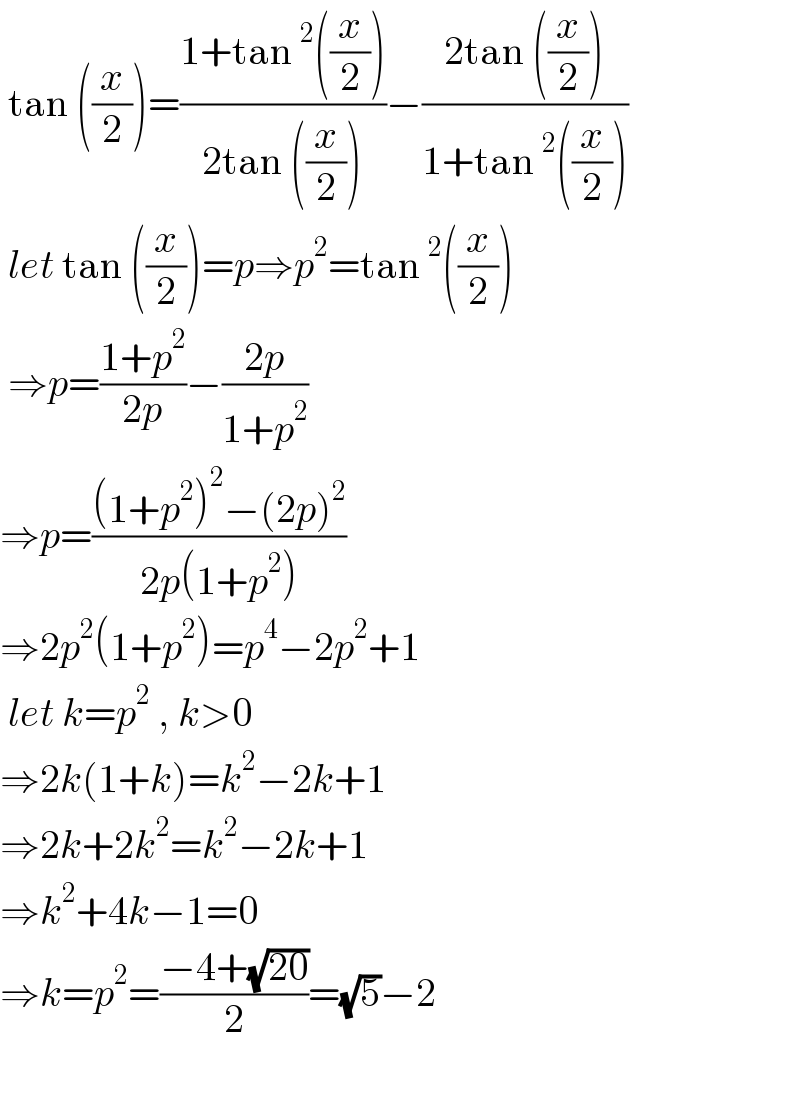
tan ((x/2))=((1+tan^2 ((x/2)))/(2tan ((x/2))))−((2tan ((x/2)))/(1+tan^2 ((x/2)))) let tan ((x/2))=p⇒p^2 =tan^2 ((x/2)) ⇒p=((1+p^2 )/(2p))−((2p)/(1+p^2 )) ⇒p=(((1+p^2 )^2 −(2p)^2 )/(2p(1+p^2 ))) ⇒2p^2 (1+p^2 )=p^4 −2p^2 +1 let k=p^2 , k>0 ⇒2k(1+k)=k^2 −2k+1 ⇒2k+2k^2 =k^2 −2k+1 ⇒k^2 +4k−1=0 ⇒k=p^2 =((−4+(√(20)))/2)=(√5)−2

$$\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)}−\frac{\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\:{let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)={p}\Rightarrow{p}^{\mathrm{2}} =\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\: \\ $$$$\:\Rightarrow{p}=\frac{\mathrm{1}+{p}^{\mathrm{2}} }{\mathrm{2}{p}}−\frac{\mathrm{2}{p}}{\mathrm{1}+{p}^{\mathrm{2}} }\: \\ $$$$\Rightarrow{p}=\frac{\left(\mathrm{1}+{p}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{2}{p}\right)^{\mathrm{2}} }{\mathrm{2}{p}\left(\mathrm{1}+{p}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{2}{p}^{\mathrm{2}} \left(\mathrm{1}+{p}^{\mathrm{2}} \right)={p}^{\mathrm{4}} −\mathrm{2}{p}^{\mathrm{2}} +\mathrm{1} \\ $$$$\:{let}\:{k}={p}^{\mathrm{2}} \:,\:{k}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{k}\left(\mathrm{1}+{k}\right)={k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{k}+\mathrm{2}{k}^{\mathrm{2}} ={k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1} \\ $$$$\Rightarrow{k}^{\mathrm{2}} +\mathrm{4}{k}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{k}={p}^{\mathrm{2}} =\frac{−\mathrm{4}+\sqrt{\mathrm{20}}}{\mathrm{2}}=\sqrt{\mathrm{5}}−\mathrm{2}\: \\ $$$$ \\ $$

Answered by Frix last updated on 17/Mar/23

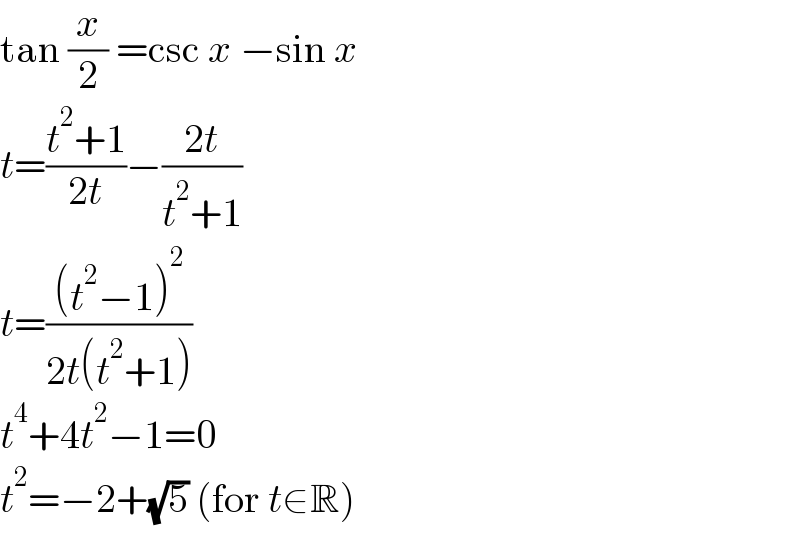
tan (x/2) =csc x −sin x t=((t^2 +1)/(2t))−((2t)/(t^2 +1)) t=(((t^2 −1)^2 )/(2t(t^2 +1))) t^4 +4t^2 −1=0 t^2 =−2+(√5) (for t∈R)

$$\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:=\mathrm{csc}\:{x}\:−\mathrm{sin}\:{x} \\ $$$${t}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}}−\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${t}=\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} =−\mathrm{2}+\sqrt{\mathrm{5}}\:\left(\mathrm{for}\:{t}\in\mathbb{R}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com