
Question Number 206434 by MATHEMATICSAM last updated on 14/Apr/24
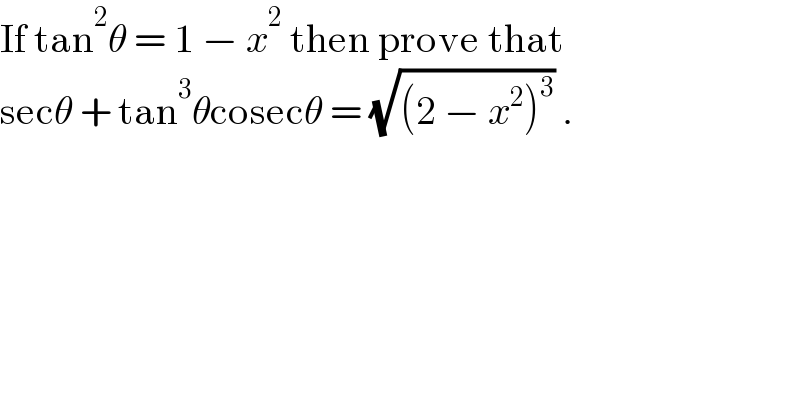
$$\mathrm{If}\:\mathrm{tan}^{\mathrm{2}} \theta\:=\:\mathrm{1}\:−\:{x}^{\mathrm{2}} \:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{sec}\theta\:+\:\mathrm{tan}^{\mathrm{3}} \theta\mathrm{cosec}\theta\:=\:\sqrt{\left(\mathrm{2}\:−\:{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:. \\ $$
Answered by TonyCWX08 last updated on 14/Apr/24
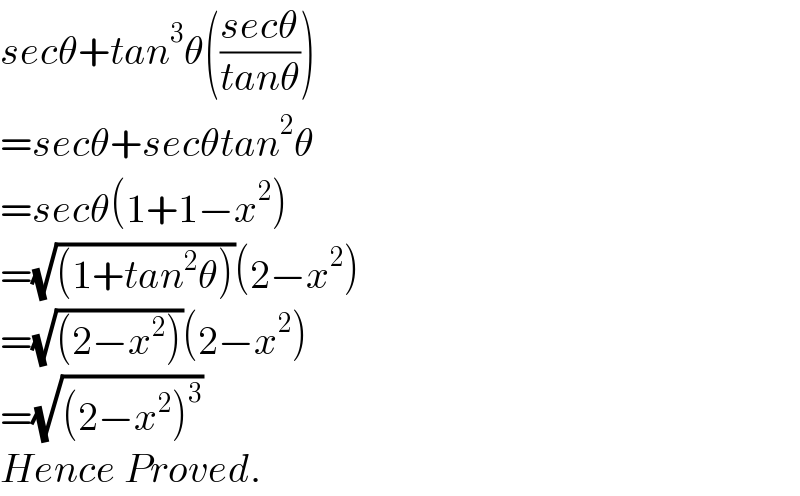
$${sec}\theta+{tan}^{\mathrm{3}} \theta\left(\frac{{sec}\theta}{{tan}\theta}\right) \\ $$$$={sec}\theta+{sec}\theta{tan}^{\mathrm{2}} \theta \\ $$$$={sec}\theta\left(\mathrm{1}+\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$=\sqrt{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}\left(\mathrm{2}−{x}^{\mathrm{2}} \right) \\ $$$$=\sqrt{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)}\left(\mathrm{2}−{x}^{\mathrm{2}} \right) \\ $$$$=\sqrt{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${Hence}\:{Proved}. \\ $$
