Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 129063 by benjo_mathlover last updated on 12/Jan/21

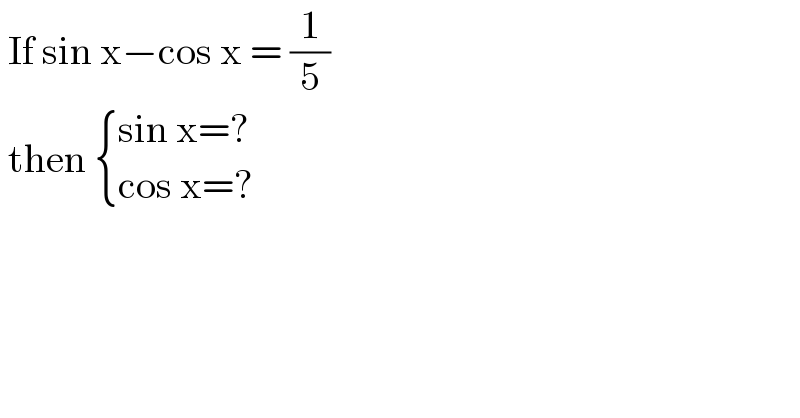
If sin x−cos x = (1/5) then { ((sin x=?)),((cos x=?)) :}

$$\:\mathrm{If}\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\:\mathrm{then}\:\begin{cases}{\mathrm{sin}\:\mathrm{x}=?}\\{\mathrm{cos}\:\mathrm{x}=?}\end{cases} \\ $$

Answered by liberty last updated on 12/Jan/21

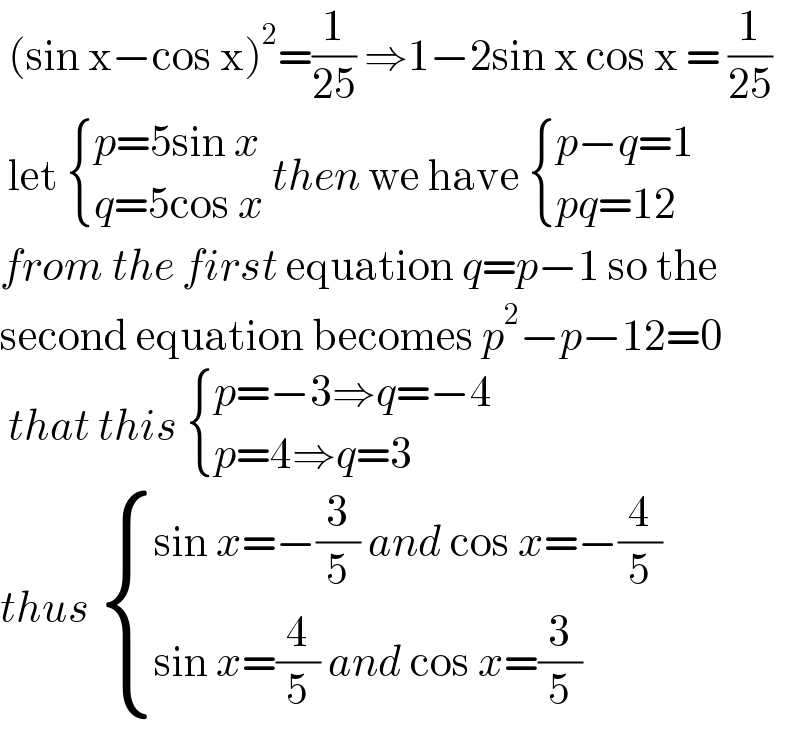
(sin x−cos x)^2 =(1/(25)) ⇒1−2sin x cos x = (1/(25)) let { ((p=5sin x)),((q=5cos x)) :} then we have { ((p−q=1)),((pq=12)) :} from the first equation q=p−1 so the second equation becomes p^2 −p−12=0 that this { ((p=−3⇒q=−4)),((p=4⇒q=3)) :} thus { ((sin x=−(3/5) and cos x=−(4/5))),((sin x=(4/5) and cos x=(3/5))) :}

$$\:\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{25}}\:\Rightarrow\mathrm{1}−\mathrm{2sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\:\mathrm{let}\:\begin{cases}{{p}=\mathrm{5sin}\:{x}}\\{{q}=\mathrm{5cos}\:{x}}\end{cases}\:{then}\:\mathrm{we}\:\mathrm{have}\:\begin{cases}{{p}−{q}=\mathrm{1}}\\{{pq}=\mathrm{12}}\end{cases} \\ $$$${from}\:{the}\:{first}\:\mathrm{equation}\:{q}={p}−\mathrm{1}\:\mathrm{so}\:\mathrm{the} \\ $$$$\mathrm{second}\:\mathrm{equation}\:\mathrm{becomes}\:{p}^{\mathrm{2}} −{p}−\mathrm{12}=\mathrm{0} \\ $$$$\:{that}\:{this}\:\begin{cases}{{p}=−\mathrm{3}\Rightarrow{q}=−\mathrm{4}}\\{{p}=\mathrm{4}\Rightarrow{q}=\mathrm{3}}\end{cases} \\ $$$${thus}\:\begin{cases}{\mathrm{sin}\:{x}=−\frac{\mathrm{3}}{\mathrm{5}}\:{and}\:\mathrm{cos}\:{x}=−\frac{\mathrm{4}}{\mathrm{5}}}\\{\mathrm{sin}\:{x}=\frac{\mathrm{4}}{\mathrm{5}}\:{and}\:\mathrm{cos}\:{x}=\frac{\mathrm{3}}{\mathrm{5}}}\end{cases} \\ $$

Answered by benjo_mathlover last updated on 12/Jan/21

Answered by MJS_new last updated on 12/Jan/21

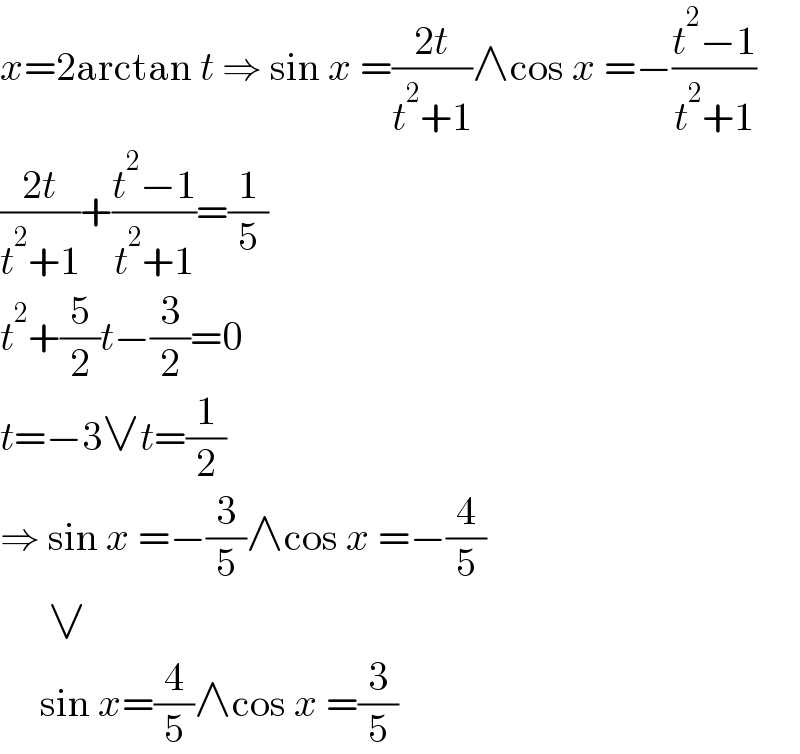
x=2arctan t ⇒ sin x =((2t)/(t^2 +1))∧cos x =−((t^2 −1)/(t^2 +1)) ((2t)/(t^2 +1))+((t^2 −1)/(t^2 +1))=(1/5) t^2 +(5/2)t−(3/2)=0 t=−3∨t=(1/2) ⇒ sin x =−(3/5)∧cos x =−(4/5) ∨ sin x=(4/5)∧cos x =(3/5)

$${x}=\mathrm{2arctan}\:{t}\:\Rightarrow\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\wedge\mathrm{cos}\:{x}\:=−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${t}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{2}}{t}−\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$${t}=−\mathrm{3}\vee{t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}\:=−\frac{\mathrm{3}}{\mathrm{5}}\wedge\mathrm{cos}\:{x}\:=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\vee \\ $$$$\:\:\:\:\:\mathrm{sin}\:{x}=\frac{\mathrm{4}}{\mathrm{5}}\wedge\mathrm{cos}\:{x}\:=\frac{\mathrm{3}}{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com