Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140477 by ajfour last updated on 08/May/21

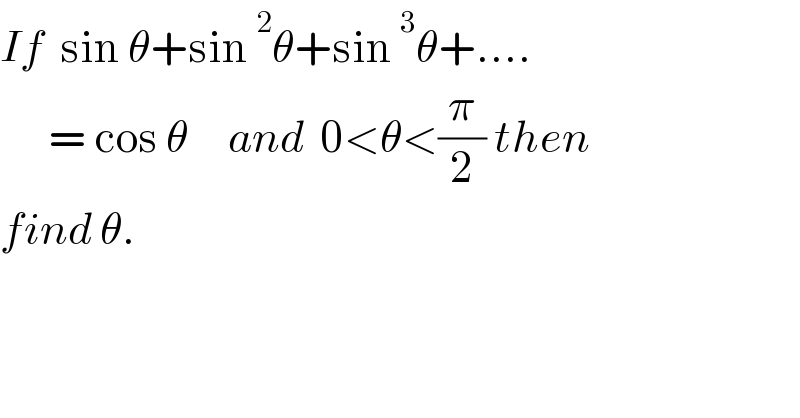
If sin θ+sin^2 θ+sin^3 θ+.... = cos θ and 0<θ<(π/2) then find θ.

$${If}\:\:\mathrm{sin}\:\theta+\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{sin}\:^{\mathrm{3}} \theta+.... \\ $$$$\:\:\:\:\:\:=\:\mathrm{cos}\:\theta\:\:\:\:\:{and}\:\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}}\:{then} \\ $$$${find}\:\theta. \\ $$

Answered by benjo_mathlover last updated on 08/May/21

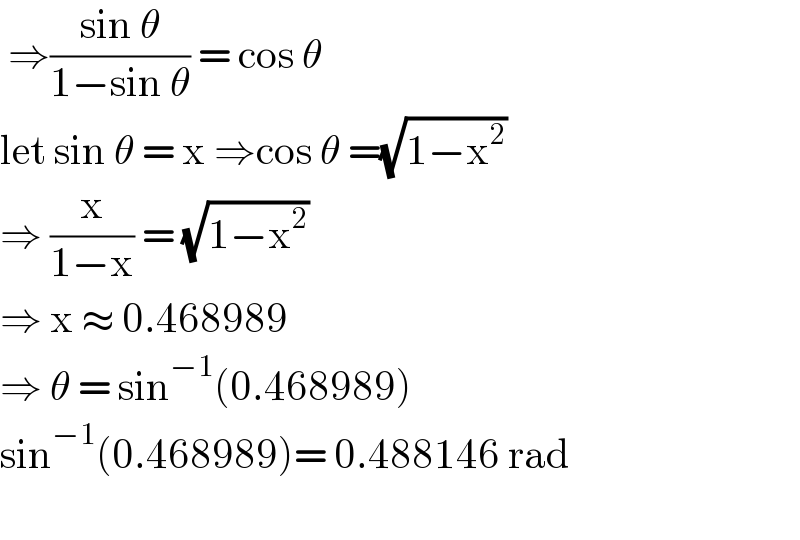
⇒((sin θ)/(1−sin θ)) = cos θ let sin θ = x ⇒cos θ =(√(1−x^2 )) ⇒ (x/(1−x)) = (√(1−x^2 )) ⇒ x ≈ 0.468989 ⇒ θ = sin^(−1) (0.468989) sin^(−1) (0.468989)= 0.488146 rad

$$\:\Rightarrow\frac{\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{sin}\:\theta}\:=\:\mathrm{cos}\:\theta \\ $$$$\mathrm{let}\:\mathrm{sin}\:\theta\:=\:\mathrm{x}\:\Rightarrow\mathrm{cos}\:\theta\:=\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\:=\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{x}\:\approx\:\mathrm{0}.\mathrm{468989} \\ $$$$\Rightarrow\:\theta\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{468989}\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{468989}\right)=\:\mathrm{0}.\mathrm{488146}\:\mathrm{rad} \\ $$$$ \\ $$

Commented by ajfour last updated on 08/May/21

Thanks sir, i also tried.

Answered by ajfour last updated on 08/May/21

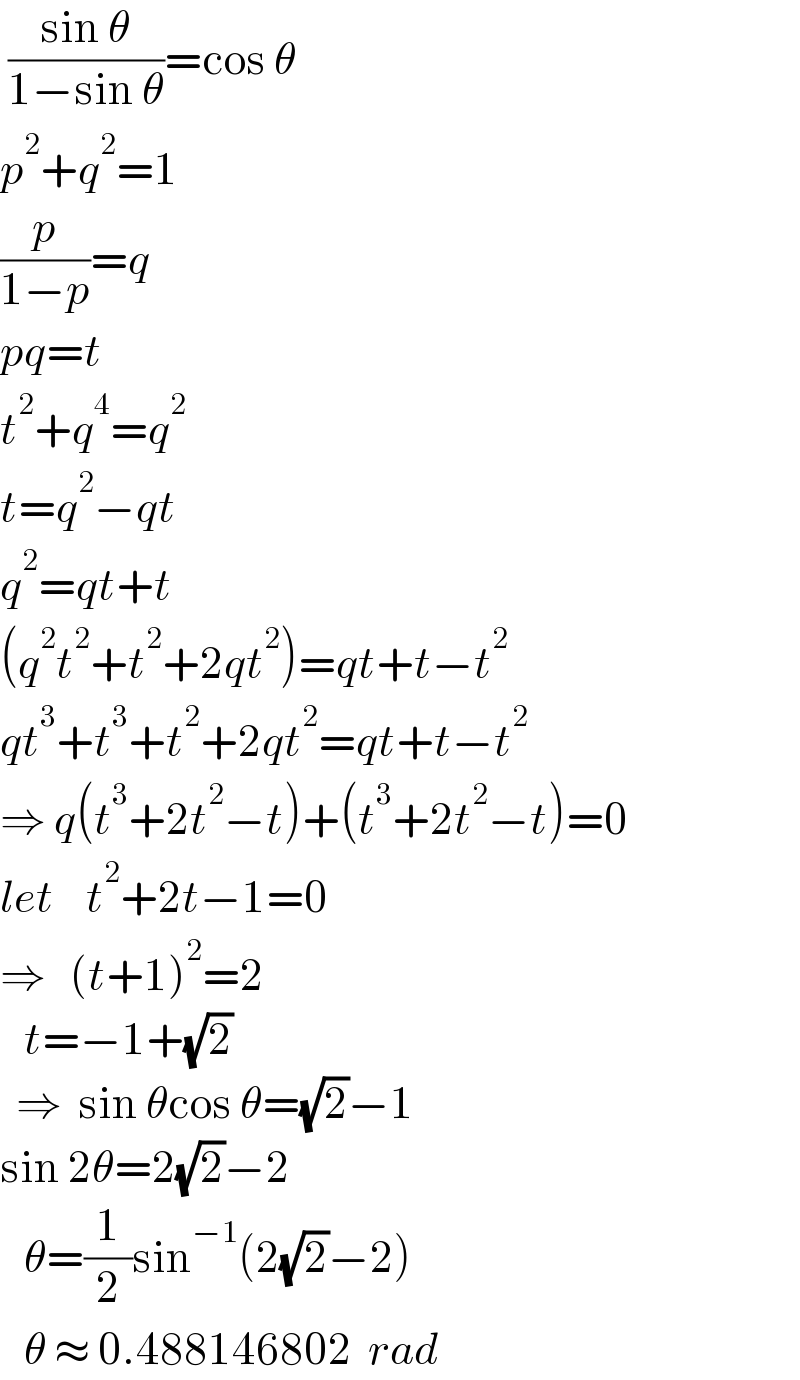
((sin θ)/(1−sin θ))=cos θ p^2 +q^2 =1 (p/(1−p))=q pq=t t^2 +q^4 =q^2 t=q^2 −qt q^2 =qt+t (q^2 t^2 +t^2 +2qt^2 )=qt+t−t^2 qt^3 +t^3 +t^2 +2qt^2 =qt+t−t^2 ⇒ q(t^3 +2t^2 −t)+(t^3 +2t^2 −t)=0 let t^2 +2t−1=0 ⇒ (t+1)^2 =2 t=−1+(√2) ⇒ sin θcos θ=(√2)−1 sin 2θ=2(√2)−2 θ=(1/2)sin^(−1) (2(√2)−2) θ ≈ 0.488146802 rad

$$\:\frac{\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{sin}\:\theta}=\mathrm{cos}\:\theta \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{{p}}{\mathrm{1}−{p}}={q} \\ $$$${pq}={t} \\ $$$${t}^{\mathrm{2}} +{q}^{\mathrm{4}} ={q}^{\mathrm{2}} \\ $$$${t}={q}^{\mathrm{2}} −{qt} \\ $$$${q}^{\mathrm{2}} ={qt}+{t} \\ $$$$\left({q}^{\mathrm{2}} {t}^{\mathrm{2}} +{t}^{\mathrm{2}} +\mathrm{2}{qt}^{\mathrm{2}} \right)={qt}+{t}−{t}^{\mathrm{2}} \\ $$$${qt}^{\mathrm{3}} +{t}^{\mathrm{3}} +{t}^{\mathrm{2}} +\mathrm{2}{qt}^{\mathrm{2}} ={qt}+{t}−{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:{q}\left({t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −{t}\right)+\left({t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −{t}\right)=\mathrm{0} \\ $$$${let}\:\:\:\:{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\left({t}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\:\:\:{t}=−\mathrm{1}+\sqrt{\mathrm{2}}\:\:\: \\ $$$$\:\:\Rightarrow\:\:\mathrm{sin}\:\theta\mathrm{cos}\:\theta=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2} \\ $$$$\:\:\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\right) \\ $$$$\:\:\:\theta\:\approx\:\mathrm{0}.\mathrm{488146802}\:\:{rad} \\ $$

Answered by mr W last updated on 08/May/21

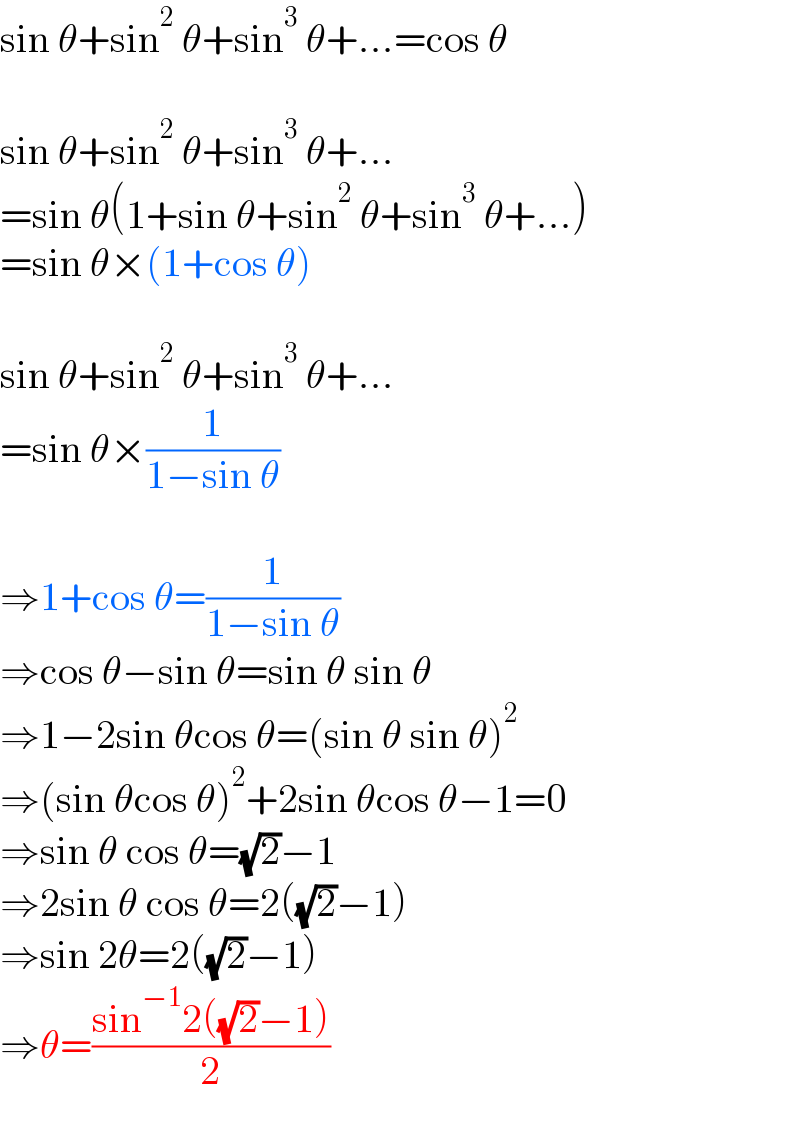
sin θ+sin^2 θ+sin^3 θ+...=cos θ sin θ+sin^2 θ+sin^3 θ+... =sin θ(1+sin θ+sin^2 θ+sin^3 θ+...) =sin θ×(1+cos θ) sin θ+sin^2 θ+sin^3 θ+... =sin θ×(1/(1−sin θ)) ⇒1+cos θ=(1/(1−sin θ)) ⇒cos θ−sin θ=sin θ sin θ ⇒1−2sin θcos θ=(sin θ sin θ)^2 ⇒(sin θcos θ)^2 +2sin θcos θ−1=0 ⇒sin θ cos θ=(√2)−1 ⇒2sin θ cos θ=2((√2)−1) ⇒sin 2θ=2((√2)−1) ⇒θ=((sin^(−1) 2((√2)−1))/2)

$$\mathrm{sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{3}} \:\theta+...=\mathrm{cos}\:\theta \\ $$$$ \\ $$$$\mathrm{sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{3}} \:\theta+... \\ $$$$=\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{3}} \:\theta+...\right) \\ $$$$=\mathrm{sin}\:\theta×\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$$ \\ $$$$\mathrm{sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{3}} \:\theta+... \\ $$$$=\mathrm{sin}\:\theta×\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\theta} \\ $$$$ \\ $$$$\Rightarrow\mathrm{1}+\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\mathrm{sin}\:\theta\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta=\left(\mathrm{sin}\:\theta\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{sin}\:\theta\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{2sin}\:\theta\mathrm{cos}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\Rightarrow\theta=\frac{\mathrm{sin}^{−\mathrm{1}} \mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 08/May/21

nice sir, you got it straight!

$${nice}\:{sir},\:{you}\:{got}\:{it}\:{straight}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com