Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 128336 by liberty last updated on 06/Jan/21

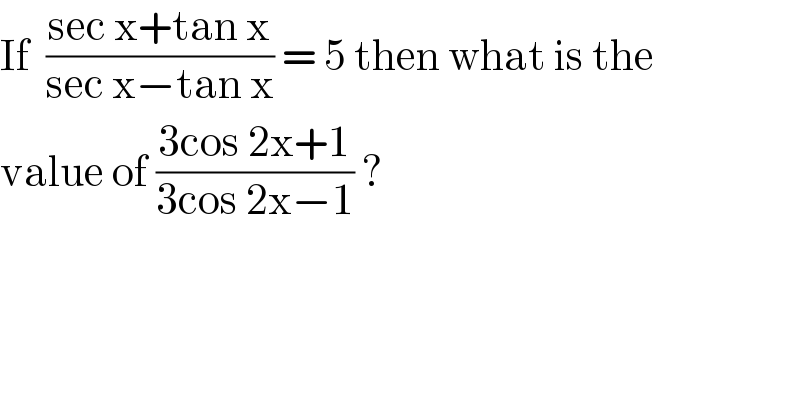
If ((sec x+tan x)/(sec x−tan x)) = 5 then what is the value of ((3cos 2x+1)/(3cos 2x−1)) ?

$$\mathrm{If}\:\:\frac{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}{\mathrm{sec}\:\mathrm{x}−\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{5}\:\mathrm{then}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{3cos}\:\mathrm{2x}+\mathrm{1}}{\mathrm{3cos}\:\mathrm{2x}−\mathrm{1}}\:?\: \\ $$

Answered by bramlexs22 last updated on 06/Jan/21

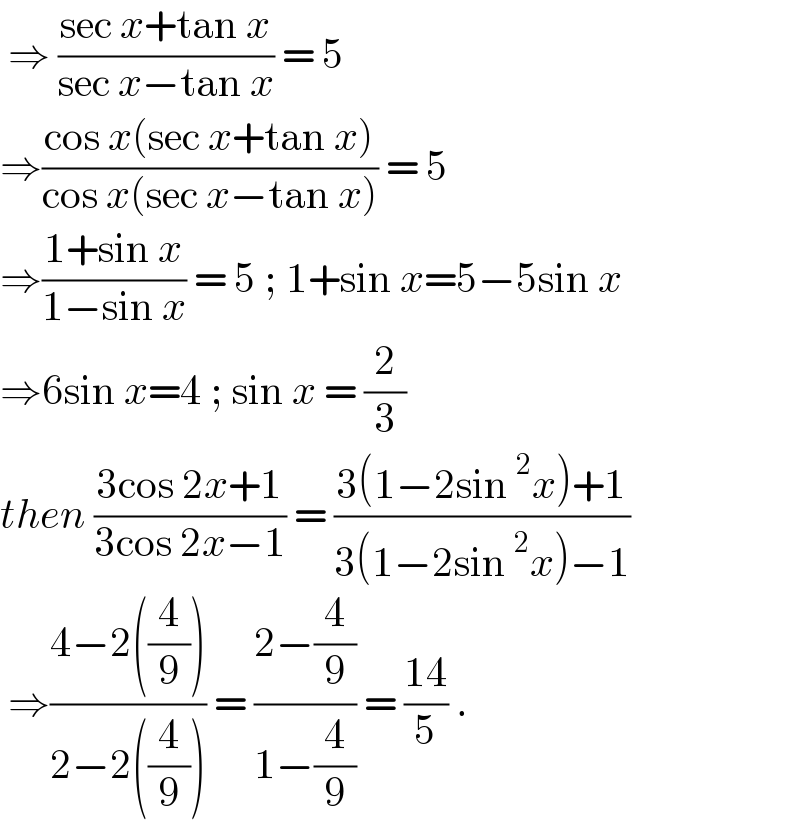
⇒ ((sec x+tan x)/(sec x−tan x)) = 5 ⇒((cos x(sec x+tan x))/(cos x(sec x−tan x))) = 5 ⇒((1+sin x)/(1−sin x)) = 5 ; 1+sin x=5−5sin x ⇒6sin x=4 ; sin x = (2/3) then ((3cos 2x+1)/(3cos 2x−1)) = ((3(1−2sin^2 x)+1)/(3(1−2sin^2 x)−1)) ⇒((4−2((4/9)))/(2−2((4/9)))) = ((2−(4/9))/(1−(4/9))) = ((14)/5) .

$$\:\Rightarrow\:\frac{\mathrm{sec}\:{x}+\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}−\mathrm{tan}\:{x}}\:=\:\mathrm{5} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:{x}\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)}{\mathrm{cos}\:{x}\left(\mathrm{sec}\:{x}−\mathrm{tan}\:{x}\right)}\:=\:\mathrm{5} \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\:=\:\mathrm{5}\:;\:\mathrm{1}+\mathrm{sin}\:{x}=\mathrm{5}−\mathrm{5sin}\:{x} \\ $$$$\Rightarrow\mathrm{6sin}\:{x}=\mathrm{4}\:;\:\mathrm{sin}\:{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${then}\:\frac{\mathrm{3cos}\:\mathrm{2}{x}+\mathrm{1}}{\mathrm{3cos}\:\mathrm{2}{x}−\mathrm{1}}\:=\:\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)+\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)−\mathrm{1}} \\ $$$$\:\Rightarrow\frac{\mathrm{4}−\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{9}}\right)}{\mathrm{2}−\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{9}}\right)}\:=\:\frac{\mathrm{2}−\frac{\mathrm{4}}{\mathrm{9}}}{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{9}}}\:=\:\frac{\mathrm{14}}{\mathrm{5}}\:.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com