Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 105766 by bramlex last updated on 31/Jul/20

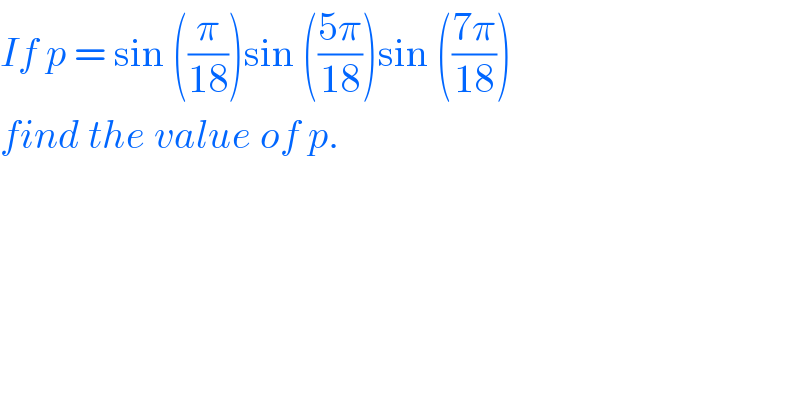
If p = sin ((π/(18)))sin (((5π)/(18)))sin (((7π)/(18))) find the value of p.

$${If}\:{p}\:=\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{18}}\right)\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{18}}\right)\mathrm{sin}\:\left(\frac{\mathrm{7}\pi}{\mathrm{18}}\right) \\ $$$${find}\:{the}\:{value}\:{of}\:{p}. \\ $$

Answered by som(math1967) last updated on 31/Jul/20

let (π/(18))=α ∴p=sinαsin5αsin7α =sinαsin (6α−α)sin (6α+α) =sin α{sin^2 6α−sin^2 α} =sin(π/(18)){sin^2 (π/3) −sin^2 (π/(18))} =sin(π/(18)){(3/4)−sin^2 (π/(18))} =(1/4)(3sin(π/(18)) −4sin^3 (π/(18))) =(1/4)×sin3.(π/(18)) =(1/4)×(1/2)=(1/8) ∴p=(1/8) ans

$$\mathrm{let}\:\frac{\pi}{\mathrm{18}}=\alpha \\ $$$$\therefore\mathrm{p}=\mathrm{sin}\alpha\mathrm{sin5}\alpha\mathrm{sin7}\alpha \\ $$$$=\mathrm{sin}\alpha\mathrm{sin}\:\left(\mathrm{6}\alpha−\alpha\right)\mathrm{sin}\:\left(\mathrm{6}\alpha+\alpha\right) \\ $$$$=\mathrm{sin}\:\alpha\left\{\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha−\mathrm{sin}^{\mathrm{2}} \alpha\right\} \\ $$$$=\mathrm{sin}\frac{\pi}{\mathrm{18}}\left\{\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{3}}\:−\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{18}}\right\} \\ $$$$=\mathrm{sin}\frac{\pi}{\mathrm{18}}\left\{\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{18}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3sin}\frac{\pi}{\mathrm{18}}\:−\mathrm{4sin}^{\mathrm{3}} \frac{\pi}{\mathrm{18}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{sin3}.\frac{\pi}{\mathrm{18}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\therefore\mathrm{p}=\frac{\mathrm{1}}{\mathrm{8}}\:\mathrm{ans} \\ $$

Commented by 1549442205PVT last updated on 01/Aug/20

Third line ⇏fourth line .Please,sir see once again and check?

$$\mathrm{Third}\:\mathrm{line}\:\nRightarrow\mathrm{fourth}\:\mathrm{line}\:.\mathrm{Please},\mathrm{sir}\:\mathrm{see} \\ $$$$\mathrm{once}\:\mathrm{again}\:\mathrm{and}\:\mathrm{check}? \\ $$

Commented by bobhans last updated on 01/Aug/20

sin α{sin 6α cos α−cos 6α sin α}{sin 6α cos α+cos 6α sin α} ⇔ sin α { (sin 6α cos α)^2 −(cos 6α sin α)^2 } sorry sir. your answer something wrong

$$\mathrm{sin}\:\alpha\left\{\mathrm{sin}\:\mathrm{6}\alpha\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\mathrm{6}\alpha\:\mathrm{sin}\:\alpha\right\}\left\{\mathrm{sin}\right. \\ $$$$\left.\mathrm{6}\alpha\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\mathrm{6}\alpha\:\mathrm{sin}\:\alpha\right\}\: \\ $$$$\Leftrightarrow\:\mathrm{sin}\:\alpha\:\left\{\:\left(\mathrm{sin}\:\mathrm{6}\alpha\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} −\left(\mathrm{cos}\:\mathrm{6}\alpha\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} \right\} \\ $$$${sorry}\:{sir}.\:{your}\:{answer}\:{something} \\ $$$${wrong} \\ $$

Commented by som(math1967) last updated on 01/Aug/20

sin(A−B)sin(A+B) =sin^2 A−sin^2 B ∴sin(6α−α)sin (6α+α) =sin^2 6α−sin^2 α α=(π/(18)) ⇒6α=(π/3) ∴sinα(sin^2 6α−sin^2 α) =sinα(sin^2 (π/3) −sin^2 α) =sinα((3/4) −sin^2 α) =sinα(((3−4sin^2 α)/4)) =((3sinα−4sin^3 α)/4) =((sin3α)/4) =((sin(π/6))/4) [∵3α=3×(π/(18))=(π/6)] =(1/4)×(1/2)=(1/8)

$$\mathrm{sin}\left(\mathrm{A}−\mathrm{B}\right)\mathrm{sin}\left(\mathrm{A}+\mathrm{B}\right) \\ $$$$=\mathrm{sin}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}^{\mathrm{2}} \mathrm{B} \\ $$$$\therefore\mathrm{sin}\left(\mathrm{6}\alpha−\alpha\right)\mathrm{sin}\:\left(\mathrm{6}\alpha+\alpha\right) \\ $$$$=\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha−\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$\alpha=\frac{\pi}{\mathrm{18}}\:\Rightarrow\mathrm{6}\alpha=\frac{\pi}{\mathrm{3}} \\ $$$$\therefore\mathrm{sin}\alpha\left(\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha−\mathrm{sin}^{\mathrm{2}} \alpha\right) \\ $$$$=\mathrm{sin}\alpha\left(\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{3}}\:−\mathrm{sin}^{\mathrm{2}} \alpha\right) \\ $$$$=\mathrm{sin}\alpha\left(\frac{\mathrm{3}}{\mathrm{4}}\:−\mathrm{sin}^{\mathrm{2}} \alpha\right) \\ $$$$=\mathrm{sin}\alpha\left(\frac{\mathrm{3}−\mathrm{4sin}^{\mathrm{2}} \alpha}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{3sin}\alpha−\mathrm{4sin}^{\mathrm{3}} \alpha}{\mathrm{4}} \\ $$$$=\frac{\mathrm{sin3}\alpha}{\mathrm{4}} \\ $$$$=\frac{\mathrm{sin}\frac{\pi}{\mathrm{6}}}{\mathrm{4}}\:\:\:\:\left[\because\mathrm{3}\alpha=\mathrm{3}×\frac{\pi}{\mathrm{18}}=\frac{\pi}{\mathrm{6}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Commented by som(math1967) last updated on 01/Aug/20

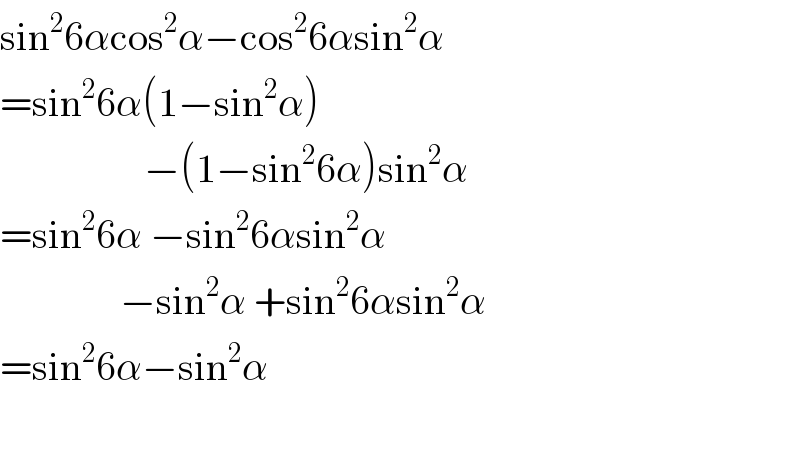
sin^2 6αcos^2 α−cos^2 6αsin^2 α =sin^2 6α(1−sin^2 α) −(1−sin^2 6α)sin^2 α =sin^2 6α −sin^2 6αsin^2 α −sin^2 α +sin^2 6αsin^2 α =sin^2 6α−sin^2 α

$$\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\mathrm{cos}^{\mathrm{2}} \alpha−\mathrm{cos}^{\mathrm{2}} \mathrm{6}\alpha\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$=\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\right)\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$=\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\:−\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sin}^{\mathrm{2}} \alpha\:+\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$=\mathrm{sin}^{\mathrm{2}} \mathrm{6}\alpha−\mathrm{sin}^{\mathrm{2}} \alpha \\ $$$$ \\ $$

Commented by bobhans last updated on 01/Aug/20

sin (A−B)sin (A+B) = −(1/2)(−2sin(A−B)sin (A+B)) −(1/2)(cos 2A−cos 2B ) = −(1/2)(1−2sin^2 A−(1−2sin^2 B)) = −(1/2)(−2sin^2 A+2sin^2 B) = sin^2 A−sin^2 B. hahaha..yes sir . you are right

$$\mathrm{sin}\:\left({A}−{B}\right)\mathrm{sin}\:\left({A}+{B}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{2sin}\left({A}−{B}\right)\mathrm{sin}\:\left({A}+{B}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{2}{A}−\mathrm{cos}\:\mathrm{2}{B}\:\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {A}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {B}\right)\right) \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{2sin}\:^{\mathrm{2}} {A}+\mathrm{2sin}\:^{\mathrm{2}} {B}\right) \\ $$$$=\:\mathrm{sin}\:^{\mathrm{2}} {A}−\mathrm{sin}\:^{\mathrm{2}} {B}.\: \\ $$$${hahaha}..{yes}\:{sir}\:.\:{you}\:{are}\:{right} \\ $$

Commented by 1549442205PVT last updated on 03/Aug/20

Thank both sirs.

$$\mathrm{Thank}\:\mathrm{both}\:\mathrm{sirs}. \\ $$

Commented by som(math1967) last updated on 01/Aug/20

Welcome

$$\mathrm{Welcome}\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com