
Question Number 75421 by peter frank last updated on 10/Dec/19
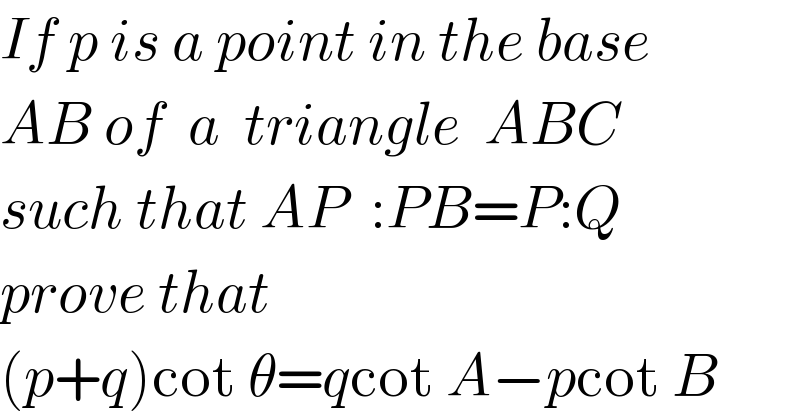
$${If}\:{p}\:{is}\:{a}\:{point}\:{in}\:{the}\:{base} \\ $$$${AB}\:{of}\:\:{a}\:\:{triangle}\:\:{ABC} \\ $$$${such}\:{that}\:{AP}\:\::{PB}={P}:{Q} \\ $$$${prove}\:{that} \\ $$$$\left({p}+{q}\right)\mathrm{cot}\:\theta={q}\mathrm{cot}\:{A}−{p}\mathrm{cot}\:{B} \\ $$
Commented by som(math1967) last updated on 11/Dec/19
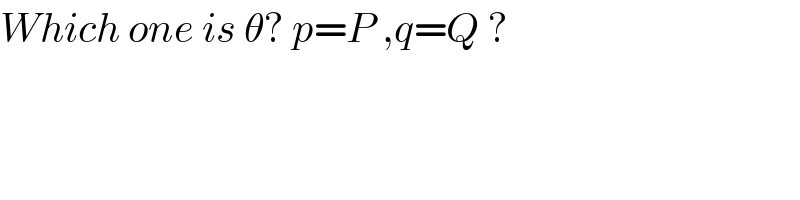
$${Which}\:{one}\:{is}\:\theta?\:{p}={P}\:,{q}={Q}\:? \\ $$
Commented by peter frank last updated on 11/Dec/19

$${p}={P} \\ $$
Commented by som(math1967) last updated on 11/Dec/19

$${Which}\:{angle}\:{is}\:\theta \\ $$
