
Question Number 63860 by gunawan last updated on 10/Jul/19

$$\mathrm{If}\:{n}\:\mathrm{is}\:\mathrm{even}\:\mathrm{positive}\:\mathrm{integer},\:\mathrm{then}\:\mathrm{the} \\ $$$$\mathrm{condition}\:\mathrm{that}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{term}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+{x}\right)^{{n}} \:\mathrm{may}\:\mathrm{have}\:\mathrm{the} \\ $$$$\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{also}\:\mathrm{is} \\ $$
Answered by mr W last updated on 10/Jul/19
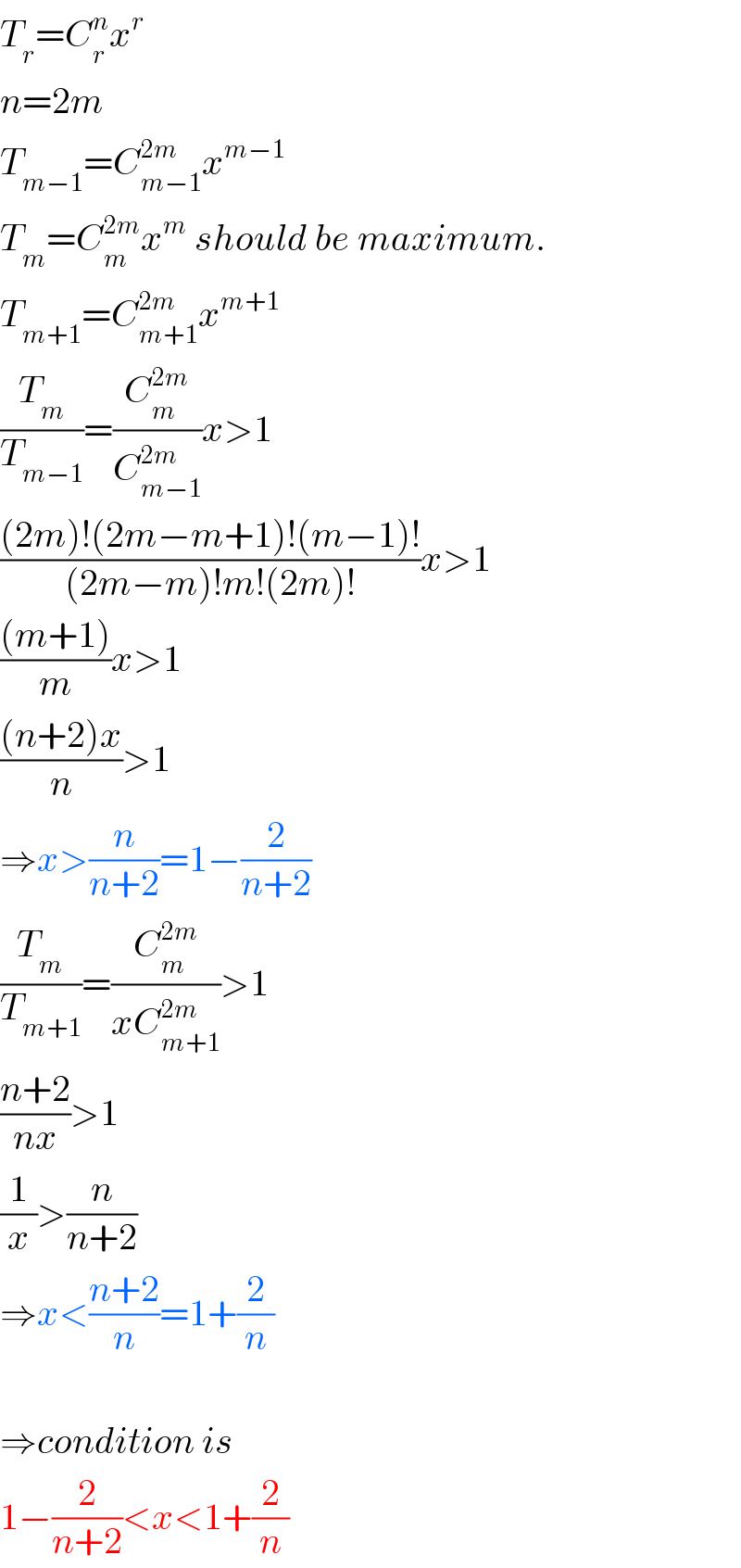
$${T}_{{r}} ={C}_{{r}} ^{{n}} {x}^{{r}} \\ $$$${n}=\mathrm{2}{m} \\ $$$${T}_{{m}−\mathrm{1}} ={C}_{{m}−\mathrm{1}} ^{\mathrm{2}{m}} {x}^{{m}−\mathrm{1}} \\ $$$${T}_{{m}} ={C}_{{m}} ^{\mathrm{2}{m}} {x}^{{m}} \:{should}\:{be}\:{maximum}. \\ $$$${T}_{{m}+\mathrm{1}} ={C}_{{m}+\mathrm{1}} ^{\mathrm{2}{m}} {x}^{{m}+\mathrm{1}} \\ $$$$\frac{{T}_{{m}} }{{T}_{{m}−\mathrm{1}} }=\frac{{C}_{{m}} ^{\mathrm{2}{m}} }{{C}_{{m}−\mathrm{1}} ^{\mathrm{2}{m}} }{x}>\mathrm{1} \\ $$$$\frac{\left(\mathrm{2}{m}\right)!\left(\mathrm{2}{m}−{m}+\mathrm{1}\right)!\left({m}−\mathrm{1}\right)!}{\left(\mathrm{2}{m}−{m}\right)!{m}!\left(\mathrm{2}{m}\right)!}{x}>\mathrm{1} \\ $$$$\frac{\left({m}+\mathrm{1}\right)}{{m}}{x}>\mathrm{1} \\ $$$$\frac{\left({n}+\mathrm{2}\right){x}}{{n}}>\mathrm{1} \\ $$$$\Rightarrow{x}>\frac{{n}}{{n}+\mathrm{2}}=\mathrm{1}−\frac{\mathrm{2}}{{n}+\mathrm{2}} \\ $$$$\frac{{T}_{{m}} }{{T}_{{m}+\mathrm{1}} }=\frac{{C}_{{m}} ^{\mathrm{2}{m}} }{{xC}_{{m}+\mathrm{1}} ^{\mathrm{2}{m}} }>\mathrm{1} \\ $$$$\frac{{n}+\mathrm{2}}{{nx}}>\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{x}}>\frac{{n}}{{n}+\mathrm{2}} \\ $$$$\Rightarrow{x}<\frac{{n}+\mathrm{2}}{{n}}=\mathrm{1}+\frac{\mathrm{2}}{{n}} \\ $$$$ \\ $$$$\Rightarrow{condition}\:{is} \\ $$$$\mathrm{1}−\frac{\mathrm{2}}{{n}+\mathrm{2}}<{x}<\mathrm{1}+\frac{\mathrm{2}}{{n}} \\ $$
