Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 53141 by gunawan last updated on 18/Jan/19

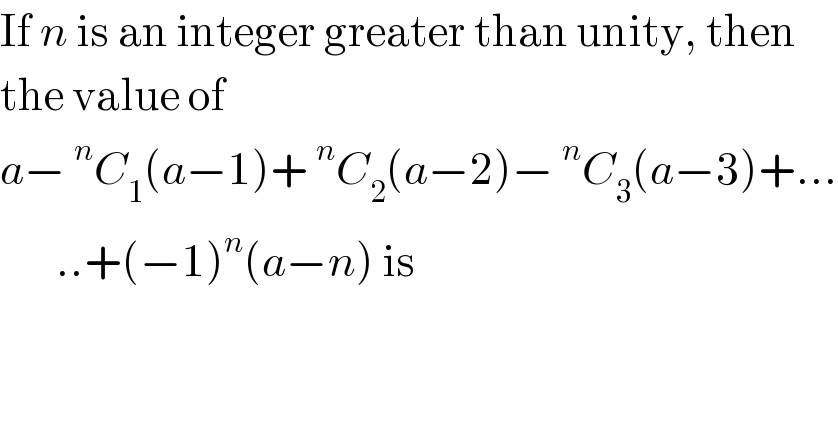
If n is an integer greater than unity, then the value of a−^n C_1 (a−1)+^n C_2 (a−2)−^n C_3 (a−3)+... ..+(−1)^n (a−n) is

$$\mathrm{If}\:{n}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{unity},\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$${a}−\:^{{n}} {C}_{\mathrm{1}} \left({a}−\mathrm{1}\right)+\:^{{n}} {C}_{\mathrm{2}} \left({a}−\mathrm{2}\right)−\:^{{n}} {C}_{\mathrm{3}} \left({a}−\mathrm{3}\right)+... \\ $$$$\:\:\:\:\:\:\:..+\left(−\mathrm{1}\right)^{{n}} \left({a}−{n}\right)\:\mathrm{is} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19

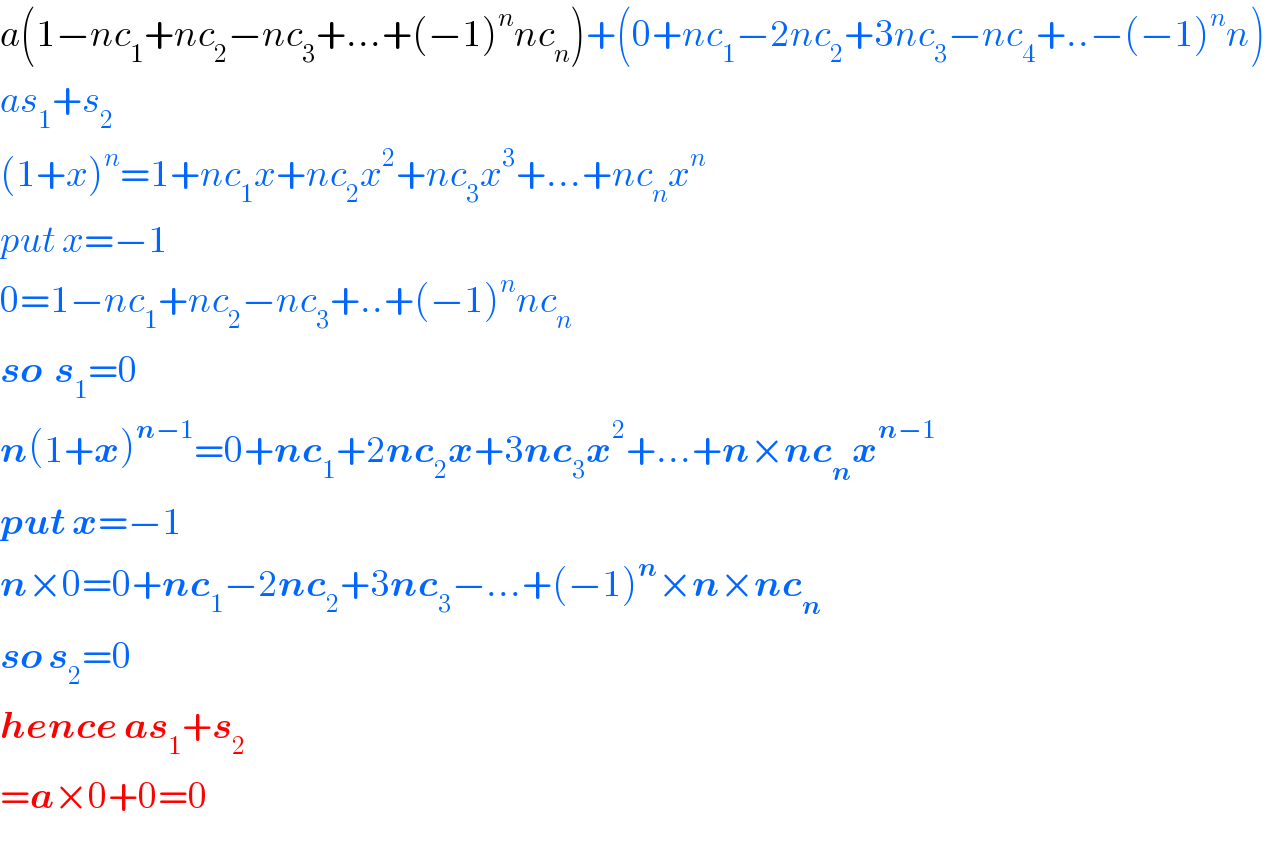
a(1−nc_1 +nc_2 −nc_3 +...+(−1)^n nc_n )+(0+nc_1 −2nc_2 +3nc_3 −nc_4 +..−(−1)^n n) as_1 +s_2 (1+x)^n =1+nc_1 x+nc_2 x^2 +nc_3 x^3 +...+nc_n x^n put x=−1 0=1−nc_1 +nc_2 −nc_3 +..+(−1)^n nc_n so s_1 =0 n(1+x)^(n−1) =0+nc_1 +2nc_2 x+3nc_3 x^2 +...+n×nc_n x^(n−1) put x=−1 n×0=0+nc_1 −2nc_2 +3nc_3 −...+(−1)^n ×n×nc_n so s_2 =0 hence as_1 +s_2 =a×0+0=0

$${a}\left(\mathrm{1}−{nc}_{\mathrm{1}} +{nc}_{\mathrm{2}} −{nc}_{\mathrm{3}} +...+\left(−\mathrm{1}\right)^{{n}} {nc}_{{n}} \right)+\left(\mathrm{0}+{nc}_{\mathrm{1}} −\mathrm{2}{nc}_{\mathrm{2}} +\mathrm{3}{nc}_{\mathrm{3}} −{nc}_{\mathrm{4}} +..−\left(−\mathrm{1}\right)^{{n}} {n}\right) \\ $$$${as}_{\mathrm{1}} +{s}_{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} =\mathrm{1}+{nc}_{\mathrm{1}} {x}+{nc}_{\mathrm{2}} {x}^{\mathrm{2}} +{nc}_{\mathrm{3}} {x}^{\mathrm{3}} +...+{nc}_{{n}} {x}^{{n}} \\ $$$${put}\:{x}=−\mathrm{1} \\ $$$$\mathrm{0}=\mathrm{1}−{nc}_{\mathrm{1}} +{nc}_{\mathrm{2}} −{nc}_{\mathrm{3}} +..+\left(−\mathrm{1}\right)^{{n}} {nc}_{{n}} \\ $$$$\boldsymbol{{so}}\:\:\boldsymbol{{s}}_{\mathrm{1}} =\mathrm{0} \\ $$$$\boldsymbol{{n}}\left(\mathrm{1}+\boldsymbol{{x}}\right)^{\boldsymbol{{n}}−\mathrm{1}} =\mathrm{0}+\boldsymbol{{nc}}_{\mathrm{1}} +\mathrm{2}\boldsymbol{{nc}}_{\mathrm{2}} \boldsymbol{{x}}+\mathrm{3}\boldsymbol{{nc}}_{\mathrm{3}} \boldsymbol{{x}}^{\mathrm{2}} +...+\boldsymbol{{n}}×\boldsymbol{{nc}}_{\boldsymbol{{n}}} \boldsymbol{{x}}^{\boldsymbol{{n}}−\mathrm{1}} \\ $$$$\boldsymbol{{put}}\:\boldsymbol{{x}}=−\mathrm{1} \\ $$$$\boldsymbol{{n}}×\mathrm{0}=\mathrm{0}+\boldsymbol{{nc}}_{\mathrm{1}} −\mathrm{2}\boldsymbol{{nc}}_{\mathrm{2}} +\mathrm{3}\boldsymbol{{nc}}_{\mathrm{3}} −...+\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} ×\boldsymbol{{n}}×\boldsymbol{{nc}}_{\boldsymbol{{n}}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{s}}_{\mathrm{2}} =\mathrm{0} \\ $$$$\boldsymbol{{hence}}\:\boldsymbol{{as}}_{\mathrm{1}} +\boldsymbol{{s}}_{\mathrm{2}} \\ $$$$=\boldsymbol{{a}}×\mathrm{0}+\mathrm{0}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com