Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 57336 by Tawa1 last updated on 02/Apr/19

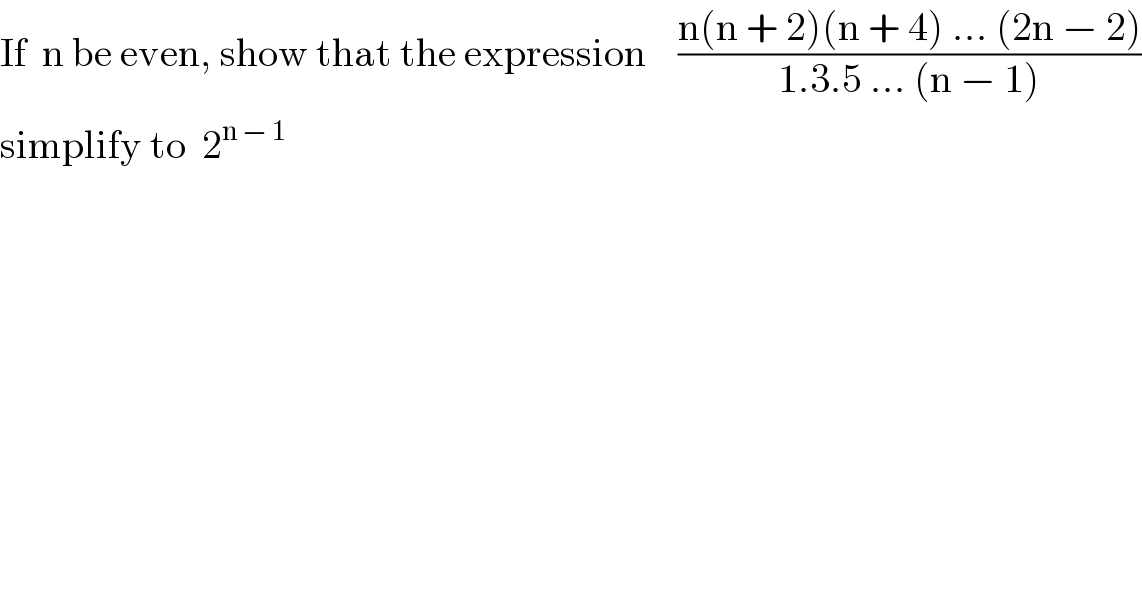
If n be even, show that the expression ((n(n + 2)(n + 4) ... (2n − 2))/(1.3.5 ... (n − 1))) simplify to 2^(n − 1)

$$\mathrm{If}\:\:\mathrm{n}\:\mathrm{be}\:\mathrm{even},\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{expression}\:\:\:\:\frac{\mathrm{n}\left(\mathrm{n}\:+\:\mathrm{2}\right)\left(\mathrm{n}\:+\:\mathrm{4}\right)\:...\:\left(\mathrm{2n}\:−\:\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}\:...\:\left(\mathrm{n}\:−\:\mathrm{1}\right)} \\ $$$$\mathrm{simplify}\:\mathrm{to}\:\:\mathrm{2}^{\mathrm{n}\:−\:\mathrm{1}} \\ $$

Answered by Smail last updated on 03/Apr/19

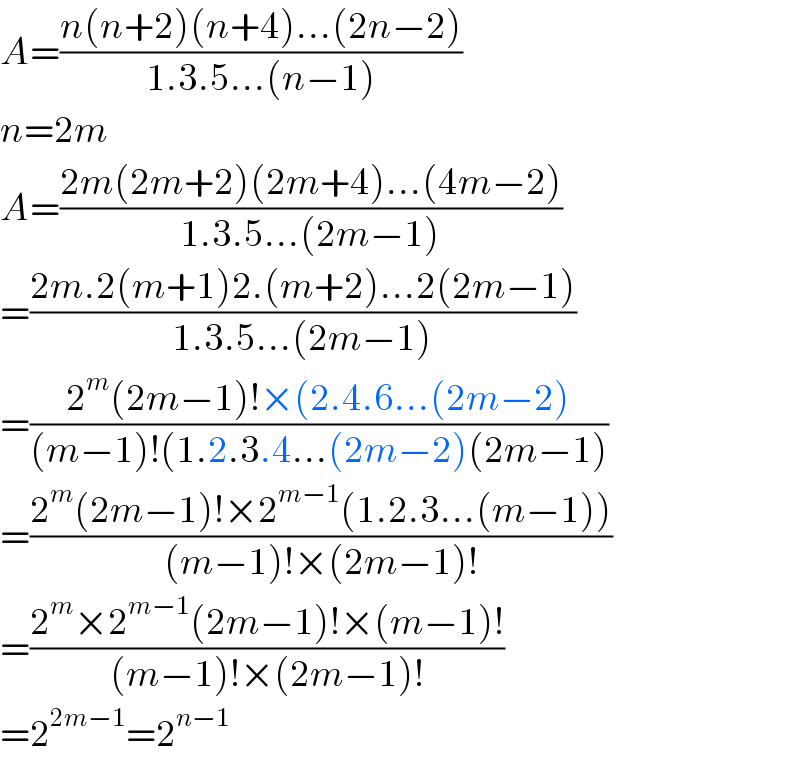
A=((n(n+2)(n+4)...(2n−2))/(1.3.5...(n−1))) n=2m A=((2m(2m+2)(2m+4)...(4m−2))/(1.3.5...(2m−1))) =((2m.2(m+1)2.(m+2)...2(2m−1))/(1.3.5...(2m−1))) =((2^m (2m−1)!×(2.4.6...(2m−2))/((m−1)!(1.2.3.4...(2m−2)(2m−1))) =((2^m (2m−1)!×2^(m−1) (1.2.3...(m−1)))/((m−1)!×(2m−1)!)) =((2^m ×2^(m−1) (2m−1)!×(m−1)!)/((m−1)!×(2m−1)!)) =2^(2m−1) =2^(n−1)

$${A}=\frac{{n}\left({n}+\mathrm{2}\right)\left({n}+\mathrm{4}\right)...\left(\mathrm{2}{n}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left({n}−\mathrm{1}\right)} \\ $$$${n}=\mathrm{2}{m} \\ $$$${A}=\frac{\mathrm{2}{m}\left(\mathrm{2}{m}+\mathrm{2}\right)\left(\mathrm{2}{m}+\mathrm{4}\right)...\left(\mathrm{4}{m}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}{m}.\mathrm{2}\left({m}+\mathrm{1}\right)\mathrm{2}.\left({m}+\mathrm{2}\right)...\mathrm{2}\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}^{{m}} \left(\mathrm{2}{m}−\mathrm{1}\right)!×\left(\mathrm{2}.\mathrm{4}.\mathrm{6}...\left(\mathrm{2}{m}−\mathrm{2}\right)\right.}{\left({m}−\mathrm{1}\right)!\left(\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}...\left(\mathrm{2}{m}−\mathrm{2}\right)\left(\mathrm{2}{m}−\mathrm{1}\right)\right.} \\ $$$$=\frac{\mathrm{2}^{{m}} \left(\mathrm{2}{m}−\mathrm{1}\right)!×\mathrm{2}^{{m}−\mathrm{1}} \left(\mathrm{1}.\mathrm{2}.\mathrm{3}...\left({m}−\mathrm{1}\right)\right)}{\left({m}−\mathrm{1}\right)!×\left(\mathrm{2}{m}−\mathrm{1}\right)!} \\ $$$$=\frac{\mathrm{2}^{{m}} ×\mathrm{2}^{{m}−\mathrm{1}} \left(\mathrm{2}{m}−\mathrm{1}\right)!×\left({m}−\mathrm{1}\right)!}{\left({m}−\mathrm{1}\right)!×\left(\mathrm{2}{m}−\mathrm{1}\right)!} \\ $$$$=\mathrm{2}^{\mathrm{2}{m}−\mathrm{1}} =\mathrm{2}^{{n}−\mathrm{1}} \\ $$

Commented by Tawa1 last updated on 03/Apr/19

God bless you sir. sir please am confused from where you started using the blue ink. I want to understand sir. Thanks for your time.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{sir}\:\mathrm{please}\:\mathrm{am}\:\mathrm{confused}\:\mathrm{from}\:\mathrm{where}\:\mathrm{you}\:\mathrm{started}\:\mathrm{using}\:\mathrm{the}\:\mathrm{blue} \\ $$$$\mathrm{ink}.\:\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Commented by Tawa1 last updated on 03/Apr/19

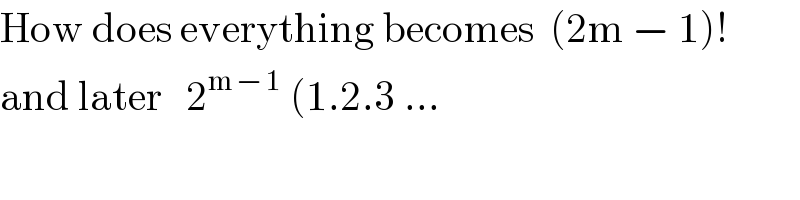
How does everything becomes (2m − 1)! and later 2^(m − 1) (1.2.3 ...

$$\mathrm{How}\:\mathrm{does}\:\mathrm{everything}\:\mathrm{becomes}\:\:\left(\mathrm{2m}\:−\:\mathrm{1}\right)! \\ $$$$\mathrm{and}\:\mathrm{later}\:\:\:\mathrm{2}^{\mathrm{m}\:−\:\mathrm{1}} \:\left(\mathrm{1}.\mathrm{2}.\mathrm{3}\:...\right. \\ $$

Commented by Kunal12588 last updated on 03/Apr/19

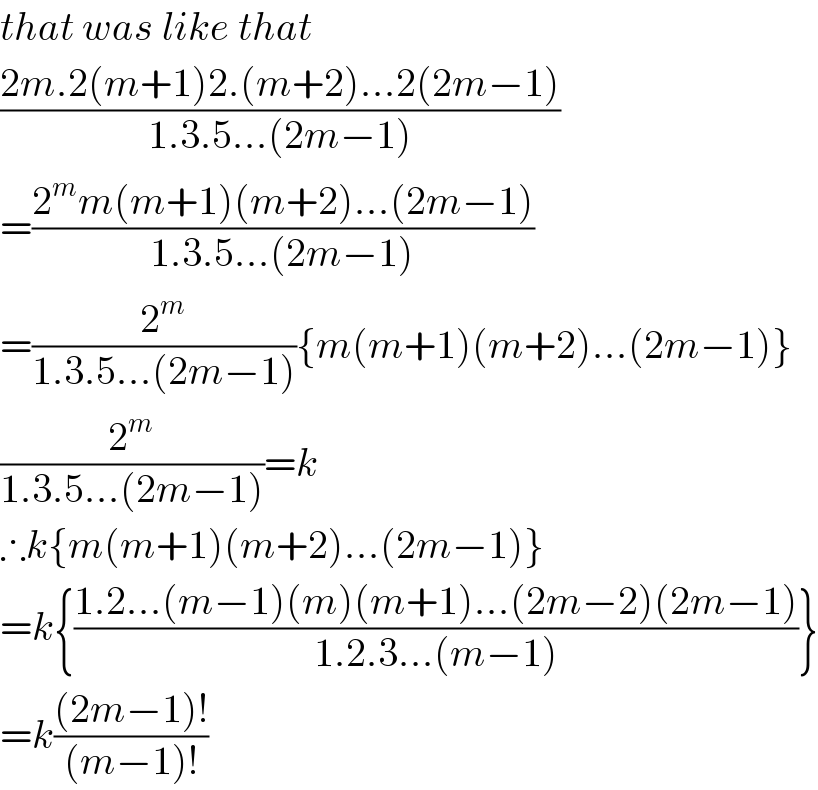
that was like that ((2m.2(m+1)2.(m+2)...2(2m−1))/(1.3.5...(2m−1))) =((2^m m(m+1)(m+2)...(2m−1))/(1.3.5...(2m−1))) =(2^m /(1.3.5...(2m−1))){m(m+1)(m+2)...(2m−1)} (2^m /(1.3.5...(2m−1)))=k ∴k{m(m+1)(m+2)...(2m−1)} =k{((1.2...(m−1)(m)(m+1)...(2m−2)(2m−1))/(1.2.3...(m−1)))} =k(((2m−1)!)/((m−1)!))

$${that}\:{was}\:{like}\:{that} \\ $$$$\frac{\mathrm{2}{m}.\mathrm{2}\left({m}+\mathrm{1}\right)\mathrm{2}.\left({m}+\mathrm{2}\right)...\mathrm{2}\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}^{{m}} {m}\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)...\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}^{{m}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)}\left\{{m}\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)...\left(\mathrm{2}{m}−\mathrm{1}\right)\right\} \\ $$$$\frac{\mathrm{2}^{{m}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{m}−\mathrm{1}\right)}={k} \\ $$$$\therefore{k}\left\{{m}\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)...\left(\mathrm{2}{m}−\mathrm{1}\right)\right\} \\ $$$$={k}\left\{\frac{\mathrm{1}.\mathrm{2}...\left({m}−\mathrm{1}\right)\left({m}\right)\left({m}+\mathrm{1}\right)...\left(\mathrm{2}{m}−\mathrm{2}\right)\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{2}.\mathrm{3}...\left({m}−\mathrm{1}\right)}\right\} \\ $$$$={k}\frac{\left(\mathrm{2}{m}−\mathrm{1}\right)!}{\left({m}−\mathrm{1}\right)!} \\ $$

Commented by Tawa1 last updated on 03/Apr/19

I appreciate sir. God bless you

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Answered by kaivan.ahmadi last updated on 02/Apr/19

by induction if n=2⇒(2/1)=2^(2−1) induction assumption if n=2k⇒((2k(2k+2)...(4k−2))/(1.3.5....(2k−1)))=2^(2k−1) now let n=2k+2⇒ (((2k+2)(2k+4).....(4k+2))/(1.3.5....(2k+1)))= ((4k(4k+2))/(2k(2k+1)))×((2k(2k+2)...(4k−2))/(1.3.5...(2k−1)))= 2×2×2^(2k−1) =2^(2k+1)

$${by}\:{induction}\:{if}\:{n}=\mathrm{2}\Rightarrow\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2}^{\mathrm{2}−\mathrm{1}} \\ $$$${induction}\:{assumption} \\ $$$${if}\:{n}=\mathrm{2}{k}\Rightarrow\frac{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{2}\right)...\left(\mathrm{4}{k}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2}{k}−\mathrm{1}\right)}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \\ $$$${now}\:{let}\:{n}=\mathrm{2}{k}+\mathrm{2}\Rightarrow \\ $$$$\frac{\left(\mathrm{2}{k}+\mathrm{2}\right)\left(\mathrm{2}{k}+\mathrm{4}\right).....\left(\mathrm{4}{k}+\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2}{k}+\mathrm{1}\right)}= \\ $$$$\frac{\mathrm{4}{k}\left(\mathrm{4}{k}+\mathrm{2}\right)}{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{1}\right)}×\frac{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{2}\right)...\left(\mathrm{4}{k}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}...\left(\mathrm{2}{k}−\mathrm{1}\right)}= \\ $$$$\mathrm{2}×\mathrm{2}×\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} =\mathrm{2}^{\mathrm{2}{k}+\mathrm{1}} \\ $$

Commented by Tawa1 last updated on 03/Apr/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com