Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 157388 by naka3546 last updated on 22/Oct/21

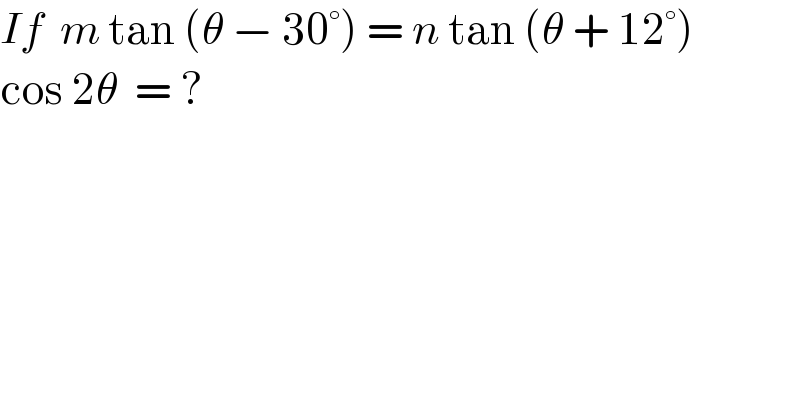
If m tan (θ − 30°) = n tan (θ + 12°) cos 2θ = ?

$${If}\:\:{m}\:\mathrm{tan}\:\left(\theta\:−\:\mathrm{30}°\right)\:=\:{n}\:\mathrm{tan}\:\left(\theta\:+\:\mathrm{12}°\right) \\ $$$$\mathrm{cos}\:\mathrm{2}\theta\:\:=\:? \\ $$

Commented by cortano last updated on 22/Oct/21

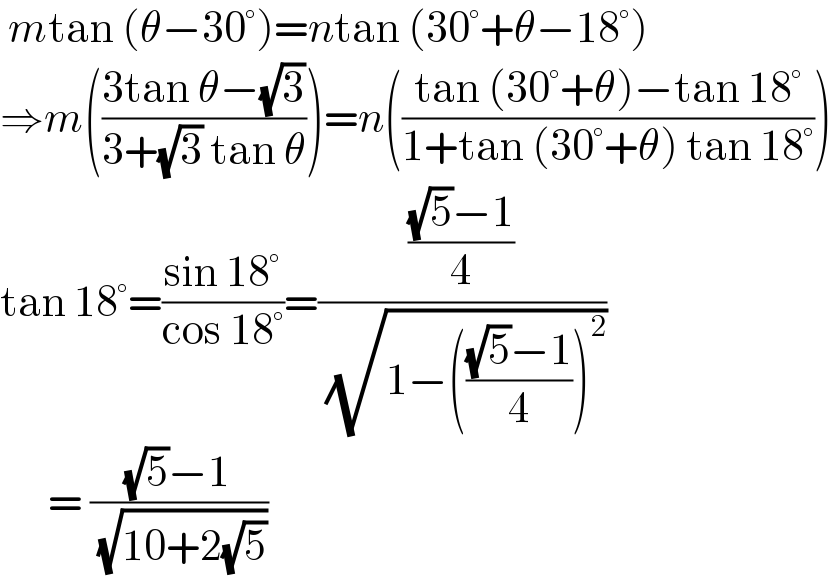
mtan (θ−30°)=ntan (30°+θ−18°) ⇒m(((3tan θ−(√3))/(3+(√3) tan θ)))=n(((tan (30°+θ)−tan 18°)/(1+tan (30°+θ) tan 18°))) tan 18°=((sin 18°)/(cos 18°))=((((√5)−1)/4)/( (√(1−((((√5)−1)/4))^2 )))) = (((√5)−1)/( (√(10+2(√5)))))

$$\:{m}\mathrm{tan}\:\left(\theta−\mathrm{30}°\right)={n}\mathrm{tan}\:\left(\mathrm{30}°+\theta−\mathrm{18}°\right) \\ $$$$\Rightarrow{m}\left(\frac{\mathrm{3tan}\:\theta−\sqrt{\mathrm{3}}}{\mathrm{3}+\sqrt{\mathrm{3}}\:\mathrm{tan}\:\theta}\right)={n}\left(\frac{\mathrm{tan}\:\left(\mathrm{30}°+\theta\right)−\mathrm{tan}\:\mathrm{18}°}{\mathrm{1}+\mathrm{tan}\:\left(\mathrm{30}°+\theta\right)\:\mathrm{tan}\:\mathrm{18}°}\right) \\ $$$$\mathrm{tan}\:\mathrm{18}°=\frac{\mathrm{sin}\:\mathrm{18}°}{\mathrm{cos}\:\mathrm{18}°}=\frac{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}}{\:\sqrt{\mathrm{1}−\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}\: \\ $$

Commented by naka3546 last updated on 23/Oct/21

thank you, sir.

$${thank}\:\:{you},\:\:{sir}. \\ $$

Answered by mr W last updated on 23/Oct/21

(m/n)tan (θ−30)=tan (θ−30+18)=((tan (θ−30)+tan 18)/(1−tan (θ−30)tan 18)) μ=(m/n), t=tan (θ−30) μt=((t+tan 18)/(1−t tan 18)) μtan 18 t^2 −(μ−1)t+tan 18=0 t=((μ−1±(√((μ−1)^2 −4μtan^2 18)))/(2μtan 18)) t=((tan θ−(1/( (√3))))/(1+((tan θ)/( (√3)))))=(((√3)tan θ−1)/(tan θ+(√3))) tan θ=((1+(√3)t)/( (√3)−t)) cos 2θ=(2/(1+tan^2 θ))−1

$$\frac{{m}}{{n}}\mathrm{tan}\:\left(\theta−\mathrm{30}\right)=\mathrm{tan}\:\left(\theta−\mathrm{30}+\mathrm{18}\right)=\frac{\mathrm{tan}\:\left(\theta−\mathrm{30}\right)+\mathrm{tan}\:\mathrm{18}}{\mathrm{1}−\mathrm{tan}\:\left(\theta−\mathrm{30}\right)\mathrm{tan}\:\mathrm{18}} \\ $$$$\mu=\frac{{m}}{{n}},\:{t}=\mathrm{tan}\:\left(\theta−\mathrm{30}\right) \\ $$$$\mu{t}=\frac{{t}+\mathrm{tan}\:\mathrm{18}}{\mathrm{1}−{t}\:\mathrm{tan}\:\mathrm{18}} \\ $$$$\mu\mathrm{tan}\:\mathrm{18}\:{t}^{\mathrm{2}} −\left(\mu−\mathrm{1}\right){t}+\mathrm{tan}\:\mathrm{18}=\mathrm{0} \\ $$$${t}=\frac{\mu−\mathrm{1}\pm\sqrt{\left(\mu−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\mu\mathrm{tan}^{\mathrm{2}} \:\mathrm{18}}}{\mathrm{2}\mu\mathrm{tan}\:\mathrm{18}} \\ $$$${t}=\frac{\mathrm{tan}\:\theta−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}=\frac{\sqrt{\mathrm{3}}\mathrm{tan}\:\theta−\mathrm{1}}{\mathrm{tan}\:\theta+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{1}+\sqrt{\mathrm{3}}{t}}{\:\sqrt{\mathrm{3}}−{t}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}−\mathrm{1} \\ $$

Commented by naka3546 last updated on 23/Oct/21

Thank you, sir.

$$\mathrm{Thank}\:\:\mathrm{you},\:\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com