Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20296 by Tinkutara last updated on 25/Aug/17

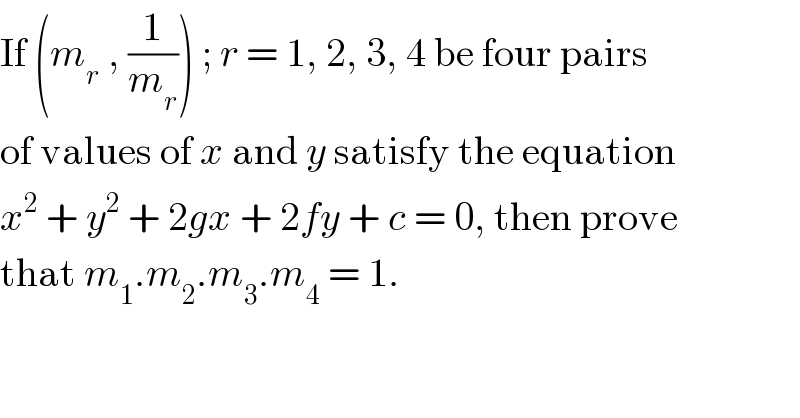
If (m_r , (1/m_r )) ; r = 1, 2, 3, 4 be four pairs of values of x and y satisfy the equation x^2 + y^2 + 2gx + 2fy + c = 0, then prove that m_1 .m_2 .m_3 .m_4 = 1.

$$\mathrm{If}\:\left({m}_{{r}} \:,\:\frac{\mathrm{1}}{{m}_{{r}} }\right)\:;\:{r}\:=\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4}\:\mathrm{be}\:\mathrm{four}\:\mathrm{pairs} \\ $$$$\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:{x}\:\mathrm{and}\:{y}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:\mathrm{2}{gx}\:+\:\mathrm{2}{fy}\:+\:{c}\:=\:\mathrm{0},\:\mathrm{then}\:\mathrm{prove} \\ $$$$\mathrm{that}\:{m}_{\mathrm{1}} .{m}_{\mathrm{2}} .{m}_{\mathrm{3}} .{m}_{\mathrm{4}} \:=\:\mathrm{1}. \\ $$

Answered by ajfour last updated on 25/Aug/17

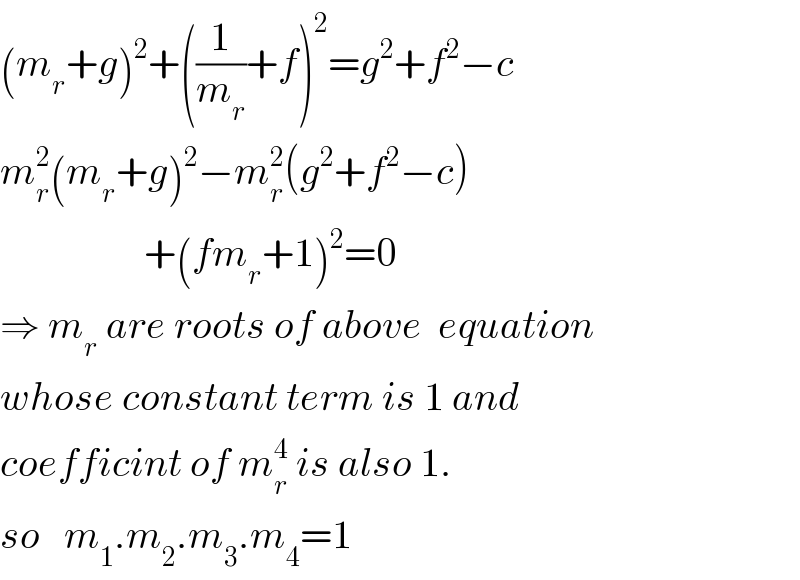
(m_r +g)^2 +((1/m_r )+f)^2 =g^2 +f^2 −c m_r ^2 (m_r +g)^2 −m_r ^2 (g^2 +f^2 −c) +(fm_r +1)^2 =0 ⇒ m_r are roots of above equation whose constant term is 1 and coefficint of m_r ^4 is also 1. so m_1 .m_2 .m_3 .m_4 =1

$$\left({m}_{{r}} +{g}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{m}_{{r}} }+{f}\right)^{\mathrm{2}} ={g}^{\mathrm{2}} +{f}^{\mathrm{2}} −{c} \\ $$$${m}_{{r}} ^{\mathrm{2}} \left({m}_{{r}} +{g}\right)^{\mathrm{2}} −{m}_{{r}} ^{\mathrm{2}} \left({g}^{\mathrm{2}} +{f}^{\mathrm{2}} −{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({fm}_{{r}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{m}_{{r}} \:{are}\:{roots}\:{of}\:{above}\:\:{equation} \\ $$$${whose}\:{constant}\:{term}\:{is}\:\mathrm{1}\:{and} \\ $$$${coefficint}\:{of}\:{m}_{{r}} ^{\mathrm{4}} \:{is}\:{also}\:\mathrm{1}. \\ $$$${so}\:\:\:{m}_{\mathrm{1}} .{m}_{\mathrm{2}} .{m}_{\mathrm{3}} .{m}_{\mathrm{4}} =\mathrm{1}\: \\ $$

Commented by Tinkutara last updated on 25/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by Tinkutara last updated on 25/Aug/17

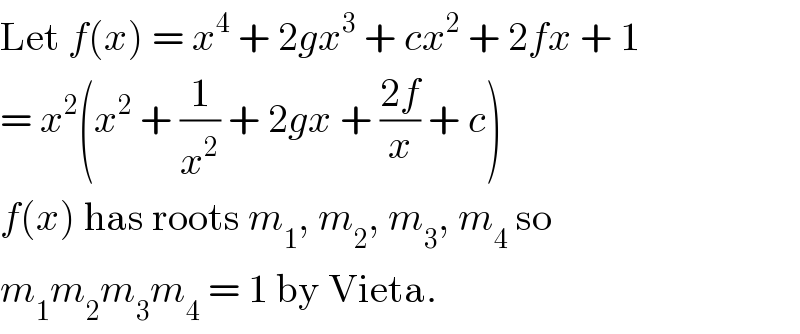
Let f(x) = x^4 + 2gx^3 + cx^2 + 2fx + 1 = x^2 (x^2 + (1/x^2 ) + 2gx + ((2f)/x) + c) f(x) has roots m_1 , m_2 , m_3 , m_4 so m_1 m_2 m_3 m_4 = 1 by Vieta.

$$\mathrm{Let}\:{f}\left({x}\right)\:=\:{x}^{\mathrm{4}} \:+\:\mathrm{2}{gx}^{\mathrm{3}} \:+\:{cx}^{\mathrm{2}} \:+\:\mathrm{2}{fx}\:+\:\mathrm{1} \\ $$$$=\:{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\mathrm{2}{gx}\:+\:\frac{\mathrm{2}{f}}{{x}}\:+\:{c}\right) \\ $$$${f}\left({x}\right)\:\mathrm{has}\:\mathrm{roots}\:{m}_{\mathrm{1}} ,\:{m}_{\mathrm{2}} ,\:{m}_{\mathrm{3}} ,\:{m}_{\mathrm{4}} \:\mathrm{so} \\ $$$${m}_{\mathrm{1}} {m}_{\mathrm{2}} {m}_{\mathrm{3}} {m}_{\mathrm{4}} \:=\:\mathrm{1}\:\mathrm{by}\:\mathrm{Vieta}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com