
Question Number 64265 by Chi Mes Try last updated on 16/Jul/19
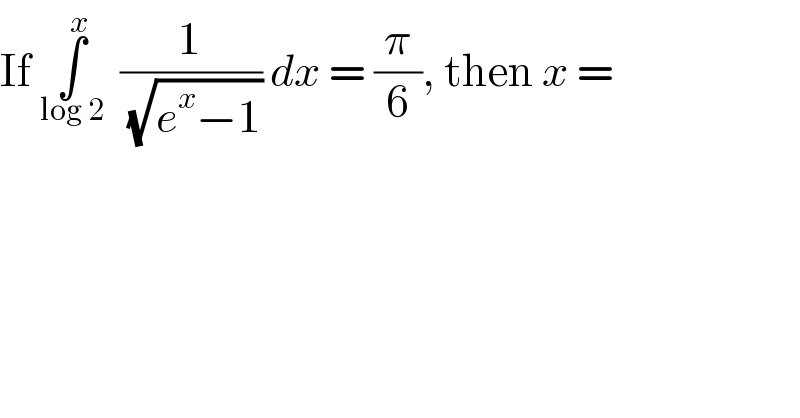
$$\mathrm{If}\:\underset{\mathrm{log}\:\mathrm{2}} {\overset{{x}} {\int}}\:\:\frac{\mathrm{1}}{\sqrt{{e}^{{x}} −\mathrm{1}}}\:{dx}\:=\:\frac{\pi}{\mathrm{6}},\:\mathrm{then}\:{x}\:= \\ $$
Commented by mathmax by abdo last updated on 17/Jul/19
![let I =∫_(ln2) ^x (dx/(√(e^x −1))) changement (√(e^x −1))=t give e^x −1=t^2 ⇒ e^x =1+t^2 ⇒x=ln(1+t^2 ) ⇒I = ∫_1 ^(√(e^x −1)) ((2t)/((1+t^2 )t)) dt =2 ∫_1 ^(√(e^x −1)) (dt/(1+t^2 )) =2[arctan(t)]_1 ^(√(e^x −1)) =2{arctan(√(e^x −1))−(π/4)} I=(π/6) ⇒2 arctan(√(e^x −1))−(π/2) =(π/6) ⇒2arctan(√(e^x −1))=(π/2) +(π/6) =((2π)/3) ⇒(√(e^x −1))=(π/3) ⇒e^x −1 =(π^2 /9) ⇒e^x =1+(π^2 /9) ⇒x =ln(1+(π^2 /9)) .](Q64360.png)
$${let}\:{I}\:=\int_{{ln}\mathrm{2}} ^{{x}} \:\:\frac{{dx}}{\sqrt{{e}^{{x}} −\mathrm{1}}}\:\:{changement}\:\sqrt{{e}^{{x}} −\mathrm{1}}={t}\:{give}\:{e}^{{x}} −\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${e}^{{x}} \:=\mathrm{1}+{t}^{\mathrm{2}} \:\Rightarrow{x}={ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:\:\Rightarrow{I}\:=\:\int_{\mathrm{1}} ^{\sqrt{{e}^{{x}} −\mathrm{1}}} \:\:\frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right){t}}\:{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{e}^{{x}} −\mathrm{1}}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\left[{arctan}\left({t}\right)\right]_{\mathrm{1}} ^{\sqrt{{e}^{{x}} −\mathrm{1}}} \:=\mathrm{2}\left\{{arctan}\sqrt{{e}^{{x}} −\mathrm{1}}−\frac{\pi}{\mathrm{4}}\right\} \\ $$$${I}=\frac{\pi}{\mathrm{6}}\:\Rightarrow\mathrm{2}\:{arctan}\sqrt{{e}^{{x}} −\mathrm{1}}−\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{6}}\:\Rightarrow\mathrm{2}{arctan}\sqrt{{e}^{{x}} −\mathrm{1}}=\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{6}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\sqrt{{e}^{{x}} −\mathrm{1}}=\frac{\pi}{\mathrm{3}}\:\Rightarrow{e}^{{x}} −\mathrm{1}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\:\Rightarrow{e}^{{x}} \:=\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\:\Rightarrow{x}\:={ln}\left(\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\right)\:. \\ $$
Commented by mathmax by abdo last updated on 17/Jul/19
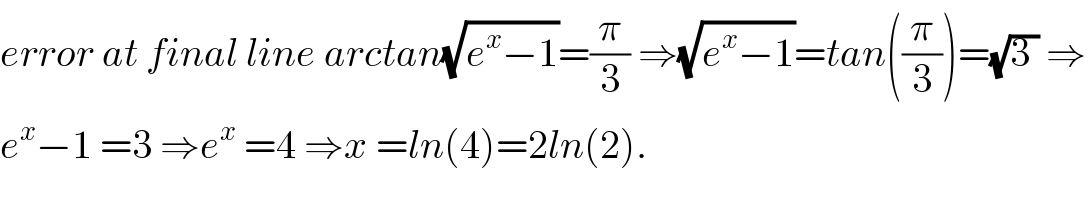
$${error}\:{at}\:{final}\:{line}\:{arctan}\sqrt{{e}^{{x}} −\mathrm{1}}=\frac{\pi}{\mathrm{3}}\:\Rightarrow\sqrt{{e}^{{x}} −\mathrm{1}}={tan}\left(\frac{\pi}{\mathrm{3}}\right)=\sqrt{\mathrm{3}\:}\:\Rightarrow \\ $$$${e}^{{x}} −\mathrm{1}\:=\mathrm{3}\:\Rightarrow{e}^{{x}} \:=\mathrm{4}\:\Rightarrow{x}\:={ln}\left(\mathrm{4}\right)=\mathrm{2}{ln}\left(\mathrm{2}\right). \\ $$
Answered by Tanmay chaudhury last updated on 16/Jul/19
![∫(dx/(√(e^x −1))) t^2 =e^x −1 2t×(dt/dx)=e^x ((2t)/(1+t^2 ))dt=dx ∫((2t)/(1+t^2 ))×(1/t)dt 2tan^(−1) (t)+c 2tan^(−1) ((√(e^x −1)) )+c ∫_0 ^x (dx/(√(e^x −1))) =2∣tan^(−1) (√(e^x −1)) ∣_(ln2) ^x =2[(tan^(−1) (√(e^x −1)) )−tan^(−1) ((√(e^(ln2) −1)) )] =2[tan^(−1) (√(e^x −1)) −(π/4)] so tan^(−1) (√(e^x −1)) =(π/(12))+(π/4) (√(e^x −1)) =tan((π/3)) e^x −1=3 e^x =4 x=ln4 Tanmay 16.07.19](Q64307.png)
$$\int\frac{{dx}}{\sqrt{{e}^{{x}} −\mathrm{1}}}\:\:\:\:\:\:{t}^{\mathrm{2}} ={e}^{{x}} −\mathrm{1}\:\:\mathrm{2}{t}×\frac{{dt}}{{dx}}={e}^{{x}} \\ $$$$\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={dx} \\ $$$$\int\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{{t}}{dt} \\ $$$$\mathrm{2}{tan}^{−\mathrm{1}} \left({t}\right)+{c} \\ $$$$\mathrm{2}{tan}^{−\mathrm{1}} \left(\sqrt{{e}^{{x}} −\mathrm{1}}\:\right)+{c} \\ $$$$\int_{\mathrm{0}} ^{{x}} \frac{{dx}}{\sqrt{{e}^{{x}} −\mathrm{1}}} \\ $$$$=\mathrm{2}\mid{tan}^{−\mathrm{1}} \sqrt{{e}^{{x}} −\mathrm{1}}\:\mid_{{ln}\mathrm{2}} ^{{x}} \\ $$$$=\mathrm{2}\left[\left({tan}^{−\mathrm{1}} \sqrt{{e}^{{x}} −\mathrm{1}}\:\right)−{tan}^{−\mathrm{1}} \left(\sqrt{{e}^{{ln}\mathrm{2}} −\mathrm{1}}\:\right)\right] \\ $$$$=\mathrm{2}\left[{tan}^{−\mathrm{1}} \sqrt{{e}^{{x}} −\mathrm{1}}\:−\frac{\pi}{\mathrm{4}}\right] \\ $$$${so}\:\:\:{tan}^{−\mathrm{1}} \sqrt{{e}^{{x}} −\mathrm{1}}\:=\frac{\pi}{\mathrm{12}}+\frac{\pi}{\mathrm{4}} \\ $$$$\sqrt{{e}^{{x}} −\mathrm{1}}\:={tan}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$${e}^{{x}} −\mathrm{1}=\mathrm{3} \\ $$$${e}^{{x}} =\mathrm{4} \\ $$$${x}={ln}\mathrm{4}\:\:\:\:\:{Tanmay}\:\:\mathrm{16}.\mathrm{07}.\mathrm{19} \\ $$
