
Question Number 115664 by bemath last updated on 27/Sep/20
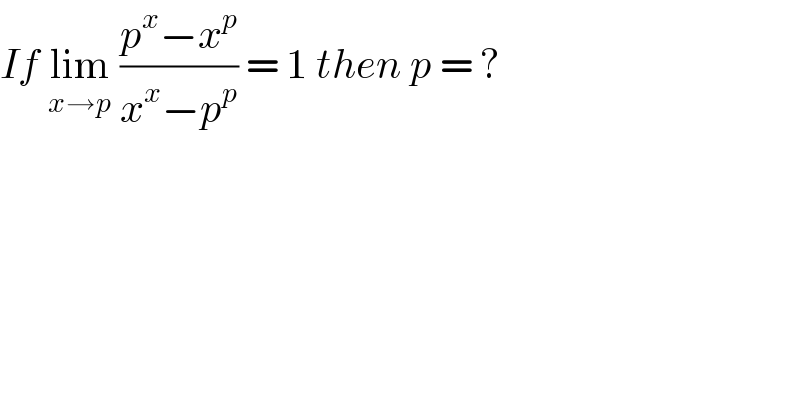
$${If}\:\underset{{x}\rightarrow{p}} {\mathrm{lim}}\:\frac{{p}^{{x}} −{x}^{{p}} }{{x}^{{x}} −{p}^{{p}} }\:=\:\mathrm{1}\:{then}\:{p}\:=\:? \\ $$
Answered by Olaf last updated on 27/Sep/20
![x = p+u lim_(x→p) ((e^(xlnp) −e^(plnx) )/(e^(xlnx) −e^(plnp) )) lim_(x→p) ((e^((xlnp+plnx)/2) (e^((xlnp−plnx)/2) −e^(−((xlnp−plnx)/2)) ))/(e^((xlnx+plnp)/2) (e^((xlnx−plnp)/2) −e^(−((xlnx−plnp)/2)) ))) lim_(x→p) e^((xln(p/x)+pln(x/p))/2) [((sinh(((xlnp−plnx)/2)))/(sinh(((xlnx−plnp)/2))))] lim_(x→p) 1×[((sinh(((xlnp−plnx)/2)))/(sinh(((xlnx−plnp)/2))))] lim_(x→p) [(((((lnp−(p/x))/2))cosh(((xlnp−plnx)/2)))/((((lnx+1)/2))cosh(((xlnx−plnp)/2))))] = ((lnp−1)/(lnp+1)) = ((ln((p/e)))/(ln(ep))) ((ln((p/e)))/(ln(ep))) = 1 ⇒ (p/e) = ep ? I′m surely wrong.](Q115672.png)
$${x}\:=\:{p}+{u} \\ $$$$\underset{{x}\rightarrow{p}} {\mathrm{lim}}\frac{{e}^{{x}\mathrm{ln}{p}} −{e}^{{p}\mathrm{ln}{x}} }{{e}^{{x}\mathrm{ln}{x}} −{e}^{{p}\mathrm{ln}{p}} } \\ $$$$\underset{{x}\rightarrow{p}} {\mathrm{lim}}\frac{{e}^{\frac{{x}\mathrm{ln}{p}+{p}\mathrm{ln}{x}}{\mathrm{2}}} \left({e}^{\frac{{x}\mathrm{ln}{p}−{p}\mathrm{ln}{x}}{\mathrm{2}}} −{e}^{−\frac{{x}\mathrm{ln}{p}−{p}\mathrm{ln}{x}}{\mathrm{2}}} \right)}{{e}^{\frac{{x}\mathrm{ln}{x}+{p}\mathrm{ln}{p}}{\mathrm{2}}} \left({e}^{\frac{{x}\mathrm{ln}{x}−{p}\mathrm{ln}{p}}{\mathrm{2}}} −{e}^{−\frac{{x}\mathrm{ln}{x}−{p}\mathrm{ln}{p}}{\mathrm{2}}} \right)} \\ $$$$\underset{{x}\rightarrow{p}} {\mathrm{lim}}\:{e}^{\frac{{x}\mathrm{ln}\frac{{p}}{{x}}+{p}\mathrm{ln}\frac{{x}}{{p}}}{\mathrm{2}}} \left[\frac{\mathrm{sinh}\left(\frac{{x}\mathrm{ln}{p}−{p}\mathrm{ln}{x}}{\mathrm{2}}\right)}{\mathrm{sinh}\left(\frac{{x}\mathrm{ln}{x}−{p}\mathrm{ln}{p}}{\mathrm{2}}\right)}\right] \\ $$$$\underset{{x}\rightarrow{p}} {\mathrm{lim}}\:\mathrm{1}×\left[\frac{\mathrm{sinh}\left(\frac{{x}\mathrm{ln}{p}−{p}\mathrm{ln}{x}}{\mathrm{2}}\right)}{\mathrm{sinh}\left(\frac{{x}\mathrm{ln}{x}−{p}\mathrm{ln}{p}}{\mathrm{2}}\right)}\right] \\ $$$$\underset{{x}\rightarrow{p}} {\mathrm{lim}}\:\left[\frac{\left(\frac{\mathrm{ln}{p}−\frac{{p}}{{x}}}{\mathrm{2}}\right)\mathrm{cosh}\left(\frac{{x}\mathrm{ln}{p}−{p}\mathrm{ln}{x}}{\mathrm{2}}\right)}{\left(\frac{\mathrm{ln}{x}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{cosh}\left(\frac{{x}\mathrm{ln}{x}−{p}\mathrm{ln}{p}}{\mathrm{2}}\right)}\right] \\ $$$$=\:\frac{\mathrm{ln}{p}−\mathrm{1}}{\mathrm{ln}{p}+\mathrm{1}}\:=\:\frac{\mathrm{ln}\left(\frac{{p}}{{e}}\right)}{\mathrm{ln}\left({ep}\right)} \\ $$$$\:\frac{\mathrm{ln}\left(\frac{{p}}{{e}}\right)}{\mathrm{ln}\left({ep}\right)}\:=\:\mathrm{1}\:\Rightarrow\:\frac{{p}}{{e}}\:=\:{ep}\:? \\ $$$$\boldsymbol{\mathrm{I}}'\boldsymbol{\mathrm{m}}\:\boldsymbol{\mathrm{surely}}\:\boldsymbol{\mathrm{wrong}}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 27/Sep/20
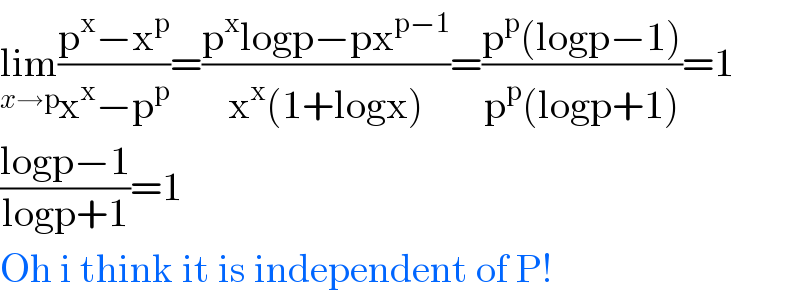
$$\underset{{x}\rightarrow\mathrm{p}} {\mathrm{lim}}\frac{\mathrm{p}^{\mathrm{x}} −\mathrm{x}^{\mathrm{p}} }{\mathrm{x}^{\mathrm{x}} −\mathrm{p}^{\mathrm{p}} }=\frac{\mathrm{p}^{\mathrm{x}} \mathrm{logp}−\mathrm{px}^{\mathrm{p}−\mathrm{1}} }{\mathrm{x}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{logx}\right)}=\frac{\mathrm{p}^{\mathrm{p}} \left(\mathrm{logp}−\mathrm{1}\right)}{\mathrm{p}^{\mathrm{p}} \left(\mathrm{logp}+\mathrm{1}\right)}=\mathrm{1} \\ $$$$\frac{\mathrm{logp}−\mathrm{1}}{\mathrm{logp}+\mathrm{1}}=\mathrm{1} \\ $$$$\mathrm{Oh}\:\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{independent}\:\mathrm{of}\:\mathrm{P}! \\ $$
