Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 11444 by Joel576 last updated on 26/Mar/17

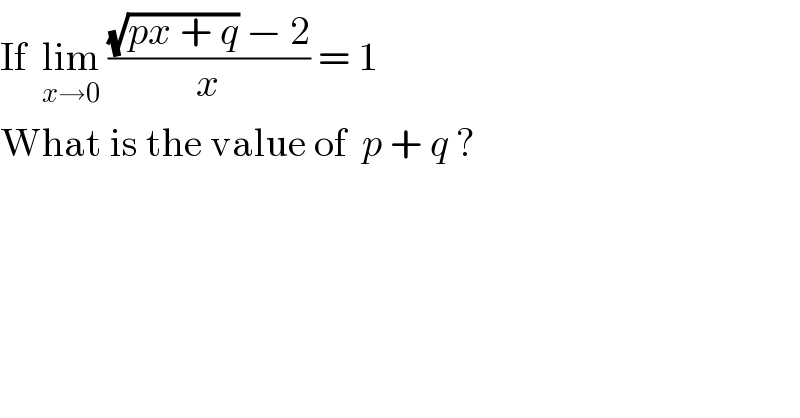
If lim_(x→0) (((√(px + q)) − 2)/x) = 1 What is the value of p + q ?

$$\mathrm{If}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{px}\:+\:{q}}\:−\:\mathrm{2}}{{x}}\:=\:\mathrm{1} \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:{p}\:+\:{q}\:? \\ $$

Answered by ajfour last updated on 26/Mar/17

then lim_(x→0) (((√q)(1+px/q)^(1/2) −2)/x) =1 ⇒ lim_(x→0) (((√q)(1+((px)/(2q)) ) −2)/x) =1 = lim_(x→0) ((((√q)−2)+(((px)/(2(√q)))))/x) =1 ⇒ (√q)=2 or q=4 then (p/(2(√q))) =1 as (√q) =2 , p=4 p+q=8

$$\mathrm{then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{q}}\left(\mathrm{1}+\mathrm{px}/\mathrm{q}\right)^{\mathrm{1}/\mathrm{2}} \:−\mathrm{2}}{\mathrm{x}}\:=\mathrm{1} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{q}}\left(\mathrm{1}+\frac{\mathrm{px}}{\mathrm{2q}}\:\right)\:−\mathrm{2}}{\mathrm{x}}\:=\mathrm{1} \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{q}}−\mathrm{2}\right)+\left(\frac{\mathrm{px}}{\mathrm{2}\sqrt{\mathrm{q}}}\right)}{\mathrm{x}}\:=\mathrm{1} \\ $$$$\Rightarrow\:\sqrt{\mathrm{q}}=\mathrm{2}\:\mathrm{or}\:\mathrm{q}=\mathrm{4} \\ $$$$\mathrm{then} \\ $$$$\frac{\mathrm{p}}{\mathrm{2}\sqrt{\mathrm{q}}}\:=\mathrm{1}\:\:\:\:\:\mathrm{as}\:\sqrt{\mathrm{q}}\:=\mathrm{2}\:,\:\:\mathrm{p}=\mathrm{4} \\ $$$$\mathrm{p}+\mathrm{q}=\mathrm{8} \\ $$

Commented by Joel576 last updated on 26/Mar/17

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Answered by ridwan balatif last updated on 26/Mar/17

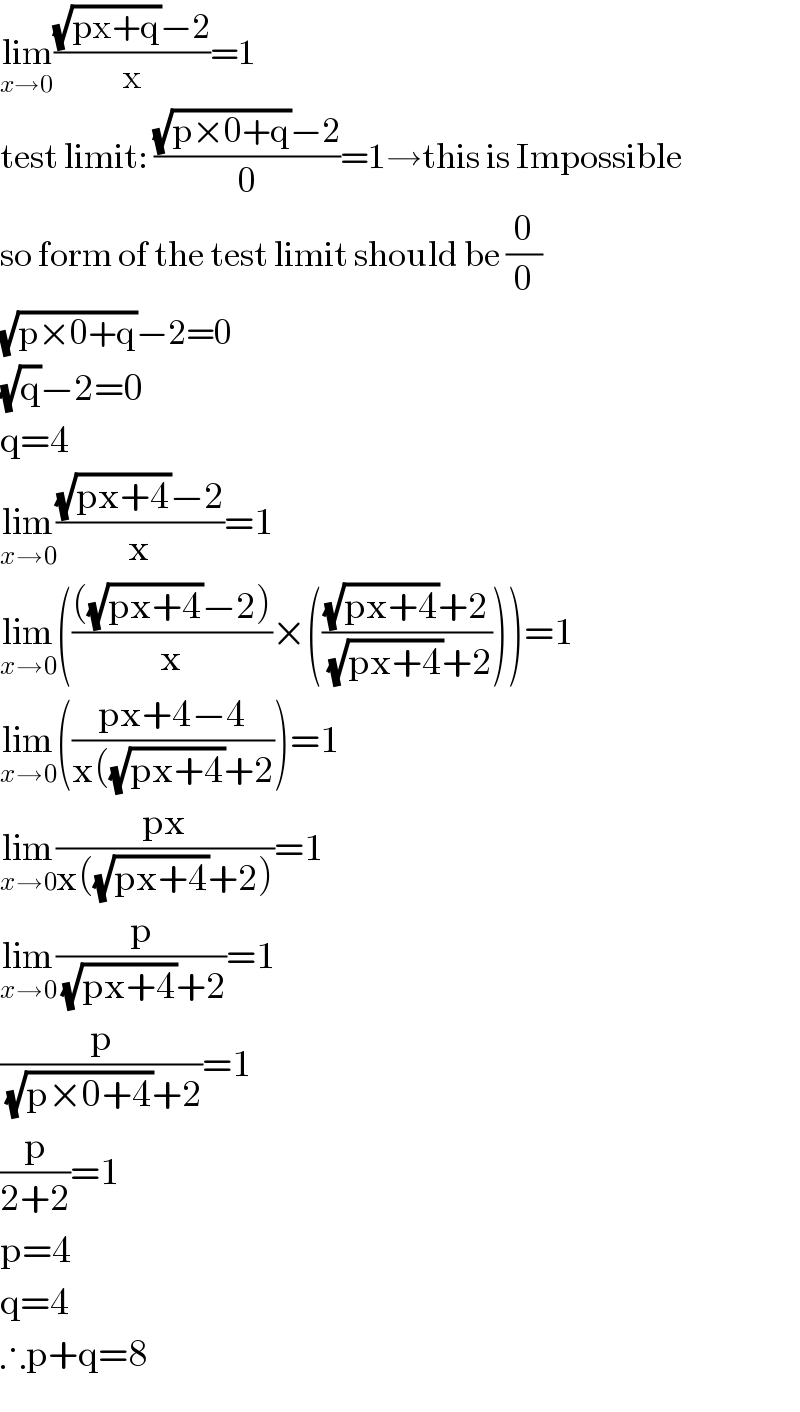
lim_(x→0) (((√(px+q))−2)/x)=1 test limit: (((√(p×0+q))−2)/0)=1→this is Impossible so form of the test limit should be (0/0) (√(p×0+q))−2=0 (√q)−2=0 q=4 lim_(x→0) (((√(px+4))−2)/x)=1 lim_(x→0) (((((√(px+4))−2))/x)×((((√(px+4))+2)/((√(px+4))+2))))=1 lim_(x→0) (((px+4−4)/(x((√(px+4))+2)))=1 lim_(x→0) ((px)/(x((√(px+4))+2)))=1 lim_(x→0) (p/((√(px+4))+2))=1 (p/((√(p×0+4))+2))=1 (p/(2+2))=1 p=4 q=4 ∴p+q=8

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{px}+\mathrm{q}}−\mathrm{2}}{\mathrm{x}}=\mathrm{1} \\ $$$$\mathrm{test}\:\mathrm{limit}:\:\frac{\sqrt{\mathrm{p}×\mathrm{0}+\mathrm{q}}−\mathrm{2}}{\mathrm{0}}=\mathrm{1}\rightarrow\mathrm{this}\:\mathrm{is}\:\mathrm{Impossible} \\ $$$$\mathrm{so}\:\mathrm{form}\:\mathrm{of}\:\mathrm{the}\:\mathrm{test}\:\mathrm{limit}\:\mathrm{should}\:\mathrm{be}\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\sqrt{\mathrm{p}×\mathrm{0}+\mathrm{q}}−\mathrm{2}=\mathrm{0} \\ $$$$\sqrt{\mathrm{q}}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{q}=\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{px}+\mathrm{4}}−\mathrm{2}}{\mathrm{x}}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\sqrt{\mathrm{px}+\mathrm{4}}−\mathrm{2}\right)}{\mathrm{x}}×\left(\frac{\sqrt{\mathrm{px}+\mathrm{4}}+\mathrm{2}}{\sqrt{\mathrm{px}+\mathrm{4}}+\mathrm{2}}\right)\right)=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{px}+\mathrm{4}−\mathrm{4}}{\mathrm{x}\left(\sqrt{\mathrm{px}+\mathrm{4}}+\mathrm{2}\right.}\right)=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{px}}{\mathrm{x}\left(\sqrt{\mathrm{px}+\mathrm{4}}+\mathrm{2}\right)}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{p}}{\sqrt{\mathrm{px}+\mathrm{4}}+\mathrm{2}}=\mathrm{1} \\ $$$$\frac{\mathrm{p}}{\sqrt{\mathrm{p}×\mathrm{0}+\mathrm{4}}+\mathrm{2}}=\mathrm{1} \\ $$$$\frac{\mathrm{p}}{\mathrm{2}+\mathrm{2}}=\mathrm{1} \\ $$$$\mathrm{p}=\mathrm{4} \\ $$$$\mathrm{q}=\mathrm{4} \\ $$$$\therefore\mathrm{p}+\mathrm{q}=\mathrm{8} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com