
Question Number 46460 by Tawa1 last updated on 26/Oct/18
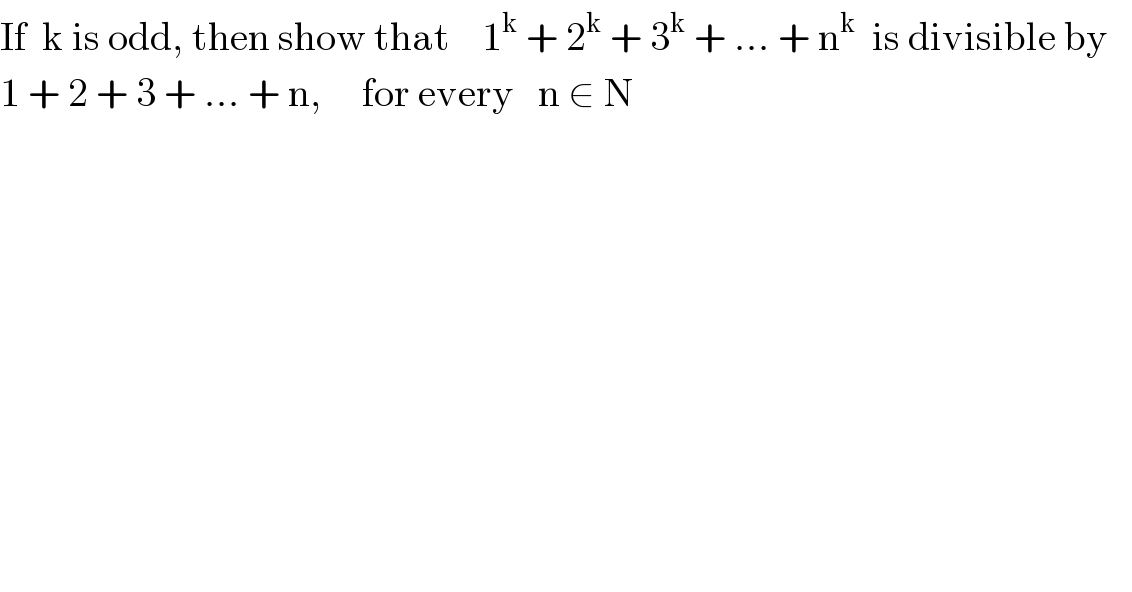
$$\mathrm{If}\:\:\mathrm{k}\:\mathrm{is}\:\mathrm{odd},\:\mathrm{then}\:\mathrm{show}\:\mathrm{that}\:\:\:\:\mathrm{1}^{\mathrm{k}} \:+\:\mathrm{2}^{\mathrm{k}} \:+\:\mathrm{3}^{\mathrm{k}} \:+\:...\:+\:\mathrm{n}^{\mathrm{k}} \:\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\:\: \\ $$$$\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:...\:+\:\mathrm{n},\:\:\:\:\:\mathrm{for}\:\mathrm{every}\:\:\:\mathrm{n}\:\in\:\mathrm{N} \\ $$
