
Question Number 185693 by Shrinava last updated on 25/Jan/23
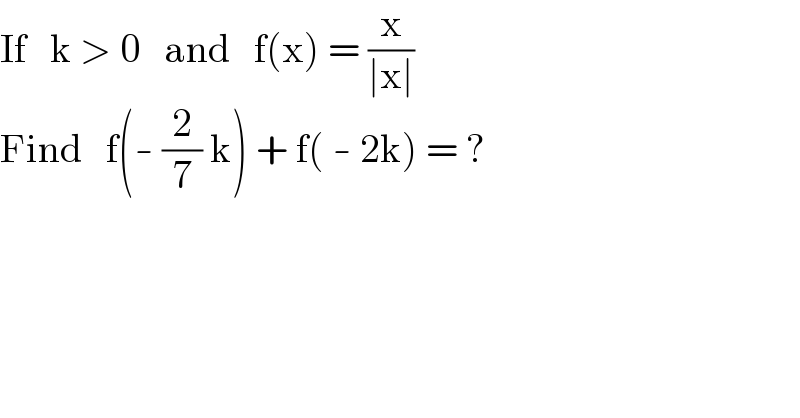
$$\mathrm{If}\:\:\:\mathrm{k}\:>\:\mathrm{0}\:\:\:\mathrm{and}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mid\mathrm{x}\mid} \\ $$$$\mathrm{Find}\:\:\:\mathrm{f}\left(-\:\frac{\mathrm{2}}{\mathrm{7}}\:\mathrm{k}\right)\:+\:\mathrm{f}\left(\:-\:\mathrm{2k}\right)\:=\:? \\ $$
Commented by Shrinava last updated on 25/Jan/23
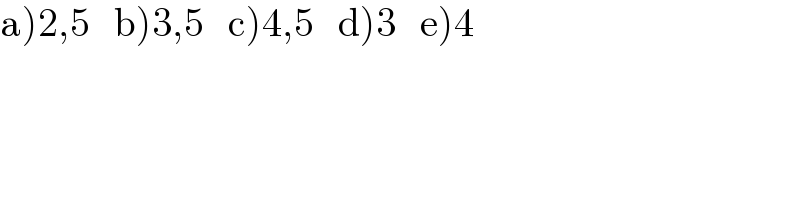
$$\left.\mathrm{a}\left.\right)\left.\mathrm{2}\left.,\left.\mathrm{5}\:\:\:\mathrm{b}\right)\mathrm{3},\mathrm{5}\:\:\:\mathrm{c}\right)\mathrm{4},\mathrm{5}\:\:\:\mathrm{d}\right)\mathrm{3}\:\:\:\mathrm{e}\right)\mathrm{4} \\ $$
Answered by HeferH last updated on 25/Jan/23
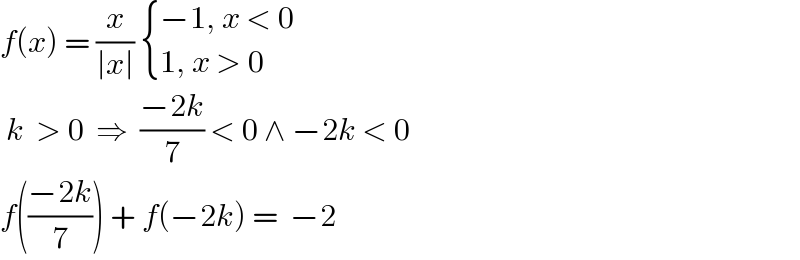
$${f}\left({x}\right)\:=\:\frac{{x}}{\mid{x}\mid}\:\begin{cases}{−\mathrm{1},\:{x}\:<\:\mathrm{0}\:}\\{\mathrm{1},\:{x}\:>\:\mathrm{0}}\end{cases} \\ $$$$\:{k}\:\:>\:\mathrm{0}\:\:\Rightarrow\:\:\frac{−\mathrm{2}{k}}{\mathrm{7}}\:<\:\mathrm{0}\:\wedge\:−\mathrm{2}{k}\:<\:\mathrm{0} \\ $$$${f}\left(\frac{−\mathrm{2}{k}}{\mathrm{7}}\right)\:+\:{f}\left(−\mathrm{2}{k}\right)\:=\:\:−\mathrm{2}\: \\ $$
