Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 127835 by bemath last updated on 02/Jan/21

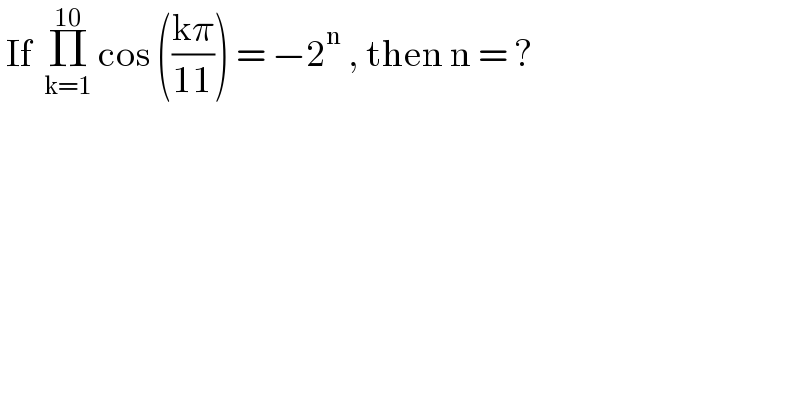
If Π_(k=1) ^(10) cos (((kπ)/(11))) = −2^n , then n = ?

$$\:\mathrm{If}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{10}} {\prod}}\:\mathrm{cos}\:\left(\frac{\mathrm{k}\pi}{\mathrm{11}}\right)\:=\:−\mathrm{2}^{\mathrm{n}} \:,\:\mathrm{then}\:\mathrm{n}\:=\:? \\ $$$$ \\ $$

Answered by liberty last updated on 02/Jan/21

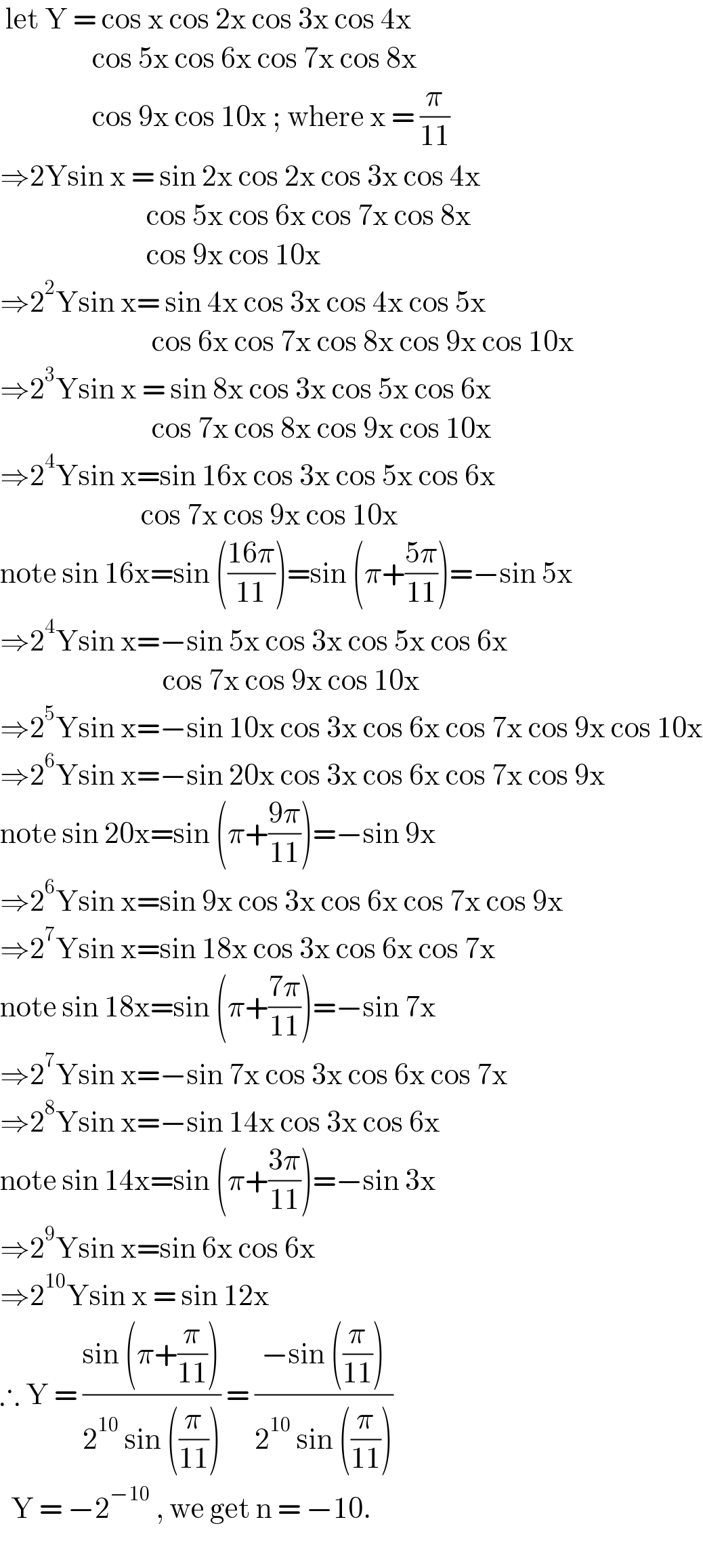
let Y = cos x cos 2x cos 3x cos 4x cos 5x cos 6x cos 7x cos 8x cos 9x cos 10x ; where x = (π/(11)) ⇒2Ysin x = sin 2x cos 2x cos 3x cos 4x cos 5x cos 6x cos 7x cos 8x cos 9x cos 10x ⇒2^2 Ysin x= sin 4x cos 3x cos 4x cos 5x cos 6x cos 7x cos 8x cos 9x cos 10x ⇒2^3 Ysin x = sin 8x cos 3x cos 5x cos 6x cos 7x cos 8x cos 9x cos 10x ⇒2^4 Ysin x=sin 16x cos 3x cos 5x cos 6x cos 7x cos 9x cos 10x note sin 16x=sin (((16π)/(11)))=sin (π+((5π)/(11)))=−sin 5x ⇒2^4 Ysin x=−sin 5x cos 3x cos 5x cos 6x cos 7x cos 9x cos 10x ⇒2^5 Ysin x=−sin 10x cos 3x cos 6x cos 7x cos 9x cos 10x ⇒2^6 Ysin x=−sin 20x cos 3x cos 6x cos 7x cos 9x note sin 20x=sin (π+((9π)/(11)))=−sin 9x ⇒2^6 Ysin x=sin 9x cos 3x cos 6x cos 7x cos 9x ⇒2^7 Ysin x=sin 18x cos 3x cos 6x cos 7x note sin 18x=sin (π+((7π)/(11)))=−sin 7x ⇒2^7 Ysin x=−sin 7x cos 3x cos 6x cos 7x ⇒2^8 Ysin x=−sin 14x cos 3x cos 6x note sin 14x=sin (π+((3π)/(11)))=−sin 3x ⇒2^9 Ysin x=sin 6x cos 6x ⇒2^(10) Ysin x = sin 12x ∴ Y = ((sin (π+(π/(11))))/(2^(10) sin ((π/(11))))) = ((−sin ((π/(11))))/(2^(10) sin ((π/(11))))) Y = −2^(−10) , we get n = −10.

$$\:\mathrm{let}\:\mathrm{Y}\:=\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{8x}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x}\:;\:\mathrm{where}\:\mathrm{x}\:=\:\frac{\pi}{\mathrm{11}} \\ $$$$\Rightarrow\mathrm{2Ysin}\:\mathrm{x}\:=\:\mathrm{sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{8x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2}} \mathrm{Ysin}\:\mathrm{x}=\:\mathrm{sin}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{5x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{8x}\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}} \mathrm{Ysin}\:\mathrm{x}\:=\:\mathrm{sin}\:\mathrm{8x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{6x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{8x}\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{4}} \mathrm{Ysin}\:\mathrm{x}=\mathrm{sin}\:\mathrm{16x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{6x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\mathrm{note}\:\mathrm{sin}\:\mathrm{16x}=\mathrm{sin}\:\left(\frac{\mathrm{16}\pi}{\mathrm{11}}\right)=\mathrm{sin}\:\left(\pi+\frac{\mathrm{5}\pi}{\mathrm{11}}\right)=−\mathrm{sin}\:\mathrm{5x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{4}} \mathrm{Ysin}\:\mathrm{x}=−\mathrm{sin}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{5x}\:\mathrm{cos}\:\mathrm{6x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{5}} \mathrm{Ysin}\:\mathrm{x}=−\mathrm{sin}\:\mathrm{10x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{10x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{6}} \mathrm{Ysin}\:\mathrm{x}=−\mathrm{sin}\:\mathrm{20x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{9x} \\ $$$$\mathrm{note}\:\mathrm{sin}\:\mathrm{20x}=\mathrm{sin}\:\left(\pi+\frac{\mathrm{9}\pi}{\mathrm{11}}\right)=−\mathrm{sin}\:\mathrm{9x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{6}} \mathrm{Ysin}\:\mathrm{x}=\mathrm{sin}\:\mathrm{9x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{9x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{7}} \mathrm{Ysin}\:\mathrm{x}=\mathrm{sin}\:\mathrm{18x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x}\: \\ $$$$\mathrm{note}\:\mathrm{sin}\:\mathrm{18x}=\mathrm{sin}\:\left(\pi+\frac{\mathrm{7}\pi}{\mathrm{11}}\right)=−\mathrm{sin}\:\mathrm{7x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{7}} \mathrm{Ysin}\:\mathrm{x}=−\mathrm{sin}\:\mathrm{7x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{7x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{8}} \mathrm{Ysin}\:\mathrm{x}=−\mathrm{sin}\:\mathrm{14x}\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{6x} \\ $$$$\mathrm{note}\:\mathrm{sin}\:\mathrm{14x}=\mathrm{sin}\:\left(\pi+\frac{\mathrm{3}\pi}{\mathrm{11}}\right)=−\mathrm{sin}\:\mathrm{3x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{9}} \mathrm{Ysin}\:\mathrm{x}=\mathrm{sin}\:\mathrm{6x}\:\mathrm{cos}\:\mathrm{6x} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{10}} \mathrm{Ysin}\:\mathrm{x}\:=\:\mathrm{sin}\:\mathrm{12x} \\ $$$$\therefore\:\mathrm{Y}\:=\:\frac{\mathrm{sin}\:\left(\pi+\frac{\pi}{\mathrm{11}}\right)}{\mathrm{2}^{\mathrm{10}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{11}}\right)}\:=\:\frac{−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{11}}\right)}{\mathrm{2}^{\mathrm{10}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{11}}\right)} \\ $$$$\:\:\mathrm{Y}\:=\:−\mathrm{2}^{−\mathrm{10}} \:,\:\mathrm{we}\:\mathrm{get}\:\mathrm{n}\:=\:−\mathrm{10}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by bemath last updated on 02/Jan/21

greatt...

$$\mathrm{greatt}... \\ $$

Commented by bemath last updated on 02/Jan/21

Terms of Service

Privacy Policy

Contact: info@tinkutara.com