Question Number 15180 by arnabpapu550@gmail.com last updated on 08/Jun/17
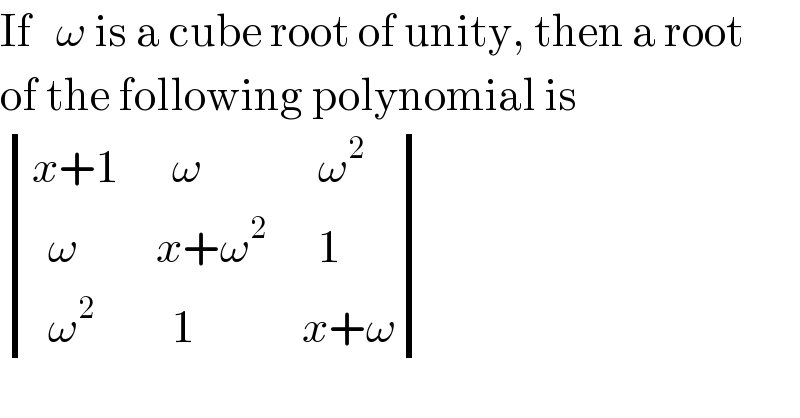
$$\mathrm{If}\:\:\:\omega\:\mathrm{is}\:\mathrm{a}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity},\:\mathrm{then}\:\mathrm{a}\:\mathrm{root} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{polynomial}\:\mathrm{is} \\ $$$$\begin{vmatrix}{{x}+\mathrm{1}}&{\:\:\omega}&{\:\:\omega^{\mathrm{2}} }\\{\:\:\omega}&{{x}+\omega^{\mathrm{2}} }&{\:\:\mathrm{1}}\\{\:\:\omega^{\mathrm{2}} }&{\:\:\mathrm{1}}&{{x}+\omega}\end{vmatrix} \\ $$
Answered by ajfour last updated on 08/Jun/17
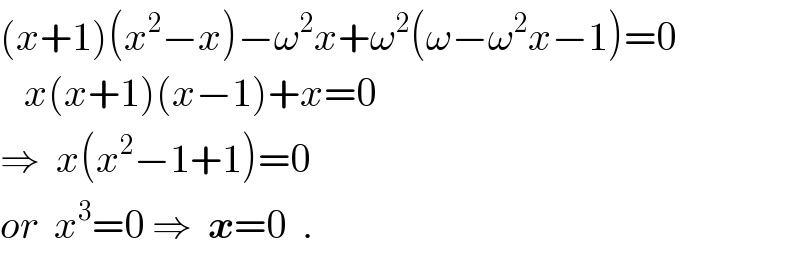
$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}\right)−\omega^{\mathrm{2}} {x}+\omega^{\mathrm{2}} \left(\omega−\omega^{\mathrm{2}} {x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:{x}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)+{x}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}\left({x}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}\right)=\mathrm{0} \\ $$$${or}\:\:{x}^{\mathrm{3}} =\mathrm{0}\:\Rightarrow\:\:\boldsymbol{{x}}=\mathrm{0}\:\:. \\ $$
Commented by arnabpapu550@gmail.com last updated on 08/Jun/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by arnabpapu550@gmail.com last updated on 08/Jun/17
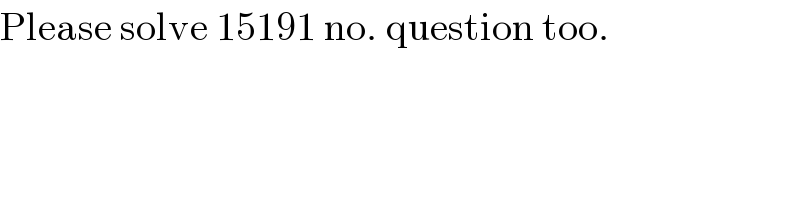
$$\mathrm{Please}\:\mathrm{solve}\:\mathrm{15191}\:\mathrm{no}.\:\mathrm{question}\:\mathrm{too}. \\ $$