
Question Number 46570 by scientist last updated on 28/Oct/18
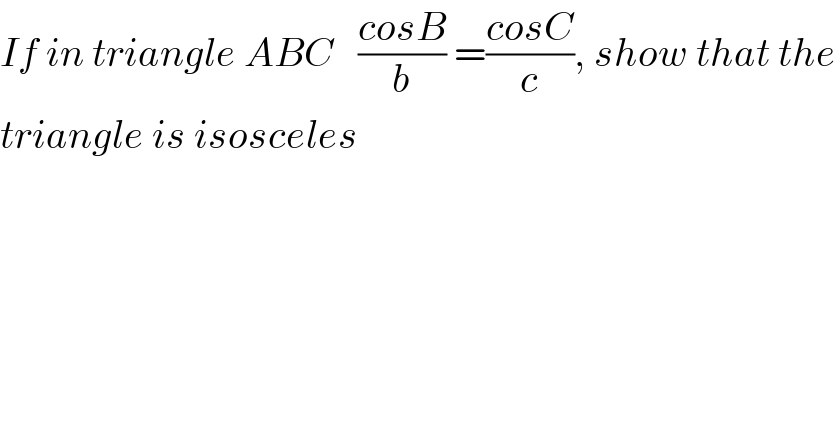
$${If}\:{in}\:{triangle}\:{ABC}\:\:\:\frac{{cosB}}{{b}}\:=\frac{{cosC}}{{c}},\:{show}\:{that}\:{the} \\ $$$${triangle}\:{is}\:{isosceles} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Oct/18
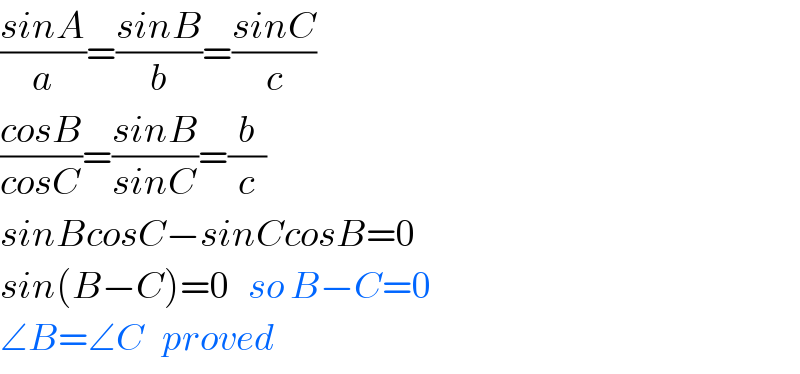
$$\frac{{sinA}}{{a}}=\frac{{sinB}}{{b}}=\frac{{sinC}}{{c}} \\ $$$$\frac{{cosB}}{{cosC}}=\frac{{sinB}}{{sinC}}=\frac{{b}}{{c}} \\ $$$${sinBcosC}−{sinCcosB}=\mathrm{0} \\ $$$${sin}\left({B}−{C}\right)=\mathrm{0}\:\:\:{so}\:{B}−{C}=\mathrm{0} \\ $$$$\angle{B}=\angle{C}\:\:\:{proved} \\ $$
