Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 106944 by Rio Michael last updated on 08/Aug/20

If Σ_(i= 1) ^n sin (θ_i ) = n then cos (θ_1 ) + cos (θ_2 ) + cos (θ_3 ) + ... + cos (θ_n ) = ? i got 0 as answer. please who can correct?

$$\mathrm{If}\:\underset{{i}=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{sin}\:\left(\theta_{{i}} \right)\:=\:{n}\:\mathrm{then}\:\:\mathrm{cos}\:\left(\theta_{\mathrm{1}} \right)\:+\:\mathrm{cos}\:\left(\theta_{\mathrm{2}} \right)\:+\:\mathrm{cos}\:\left(\theta_{\mathrm{3}} \right)\:+\:...\:+\:\mathrm{cos}\:\left(\theta_{{n}} \right)\:=\:? \\ $$$$\mathrm{i}\:\mathrm{got}\:\mathrm{0}\:\mathrm{as}\:\mathrm{answer}.\:\mathrm{please}\:\mathrm{who}\:\mathrm{can}\:\mathrm{correct}? \\ $$

Commented by mr W last updated on 08/Aug/20

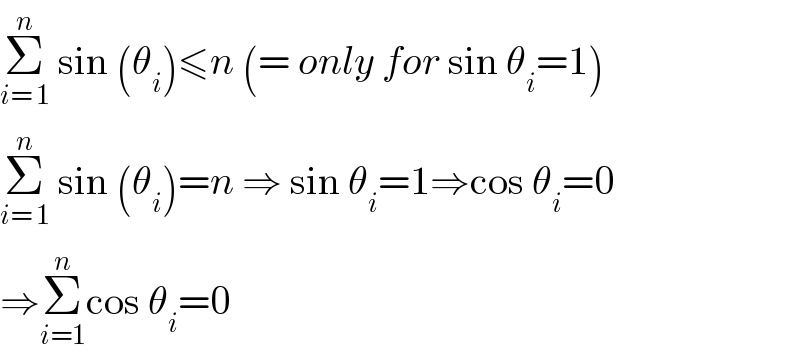
Σ_(i= 1) ^n sin (θ_i )≤n (= only for sin θ_i =1) Σ_(i= 1) ^n sin (θ_i )=n ⇒ sin θ_i =1⇒cos θ_i =0 ⇒Σ_(i=1) ^n cos θ_i =0

$$\underset{{i}=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{sin}\:\left(\theta_{{i}} \right)\leqslant{n}\:\left(=\:{only}\:{for}\:\mathrm{sin}\:\theta_{{i}} =\mathrm{1}\right) \\ $$$$\underset{{i}=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\mathrm{sin}\:\left(\theta_{{i}} \right)={n}\:\Rightarrow\:\mathrm{sin}\:\theta_{{i}} =\mathrm{1}\Rightarrow\mathrm{cos}\:\theta_{{i}} =\mathrm{0} \\ $$$$\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:\theta_{{i}} =\mathrm{0} \\ $$

Commented by Rio Michael last updated on 08/Aug/20

thanks to you both sirs

$$\mathrm{thanks}\:\mathrm{to}\:\mathrm{you}\:\mathrm{both}\:\mathrm{sirs} \\ $$

Answered by 1549442205PVT last updated on 08/Aug/20

Applying the inequality AM−GM We have n=Σ_(k=1) ^(n) cosθ_k =Σ_(k=1) ^(n) (√(1−sin^2 θ_k )) =1.(√(1−sin^2 θ_1 )) +1.(√(1−sin^2 θ_2 )) +...+1.(√(1−sin^2 θ_n )) ≤(√((1+1+..+1)(1−sin^2 θ_1 +1−sin^2 θ_2 +...+1−sin^2 θ_n ))) =(√(n(cos^2 θ_1 +cos^2 θ_2 +...+cos^2 θ_n ))) ≤(√(n.n))=n (since cosθ_k ^2 ≤1 ∀k=1...n^(−) ) This shows that the above inequality must ocurr equality sign which is equivalent to { (((1/(1−sin^2 θ_1 ))=(1/(1−sin^2 θ_2 ))=...=(1/(1−sin^2 θ_n )))),((sinθ_1 +sinθ_2 +...+sinθ_n =n)) :} ⇔ { ((sinθ_1 =sinθ_2 = ... =sinθ_n )),((sinθ_1 +sinθ_2 + ... +sinθ_n =n)) :} ⇔sinθ_1 =sinθ_2 = ... =sinθ_n =1 ⇔cosθ_1 =cosθ_2 = ... =cosθ_n =0 ⇒Σ_(k=1) ^(n) cos(θ_k )=0(q.e.d)

$$\mathrm{Applying}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{AM}−\mathrm{GM} \\ $$$$\mathrm{We}\:\mathrm{have}\:\:\:\:\mathrm{n}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{cos}\theta_{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{k}} } \\ $$$$=\mathrm{1}.\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{1}} }\:+\mathrm{1}.\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{2}} }\:+...+\mathrm{1}.\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{n}} \:} \\ $$$$\leqslant\sqrt{\left(\mathrm{1}+\mathrm{1}+..+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{1}} +\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{2}} +...+\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{n}} \right)} \\ $$$$=\sqrt{\mathrm{n}\left(\mathrm{cos}^{\mathrm{2}} \theta_{\mathrm{1}} +\mathrm{cos}^{\mathrm{2}} \theta_{\mathrm{2}} +...+\mathrm{cos}^{\mathrm{2}} \theta_{\mathrm{n}} \right)} \\ $$$$\leqslant\sqrt{\mathrm{n}.\mathrm{n}}=\mathrm{n}\:\left(\mathrm{since}\:\mathrm{cos}\theta_{\mathrm{k}} ^{\mathrm{2}} \:\leqslant\mathrm{1}\:\forall\mathrm{k}=\overline {\mathrm{1}...\mathrm{n}}\right) \\ $$$$\mathrm{This}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{above}\:\mathrm{inequality} \\ $$$$\mathrm{must}\:\:\mathrm{ocurr}\:\:\mathrm{equality}\:\mathrm{sign}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{equivalent}\:\mathrm{to} \\ $$$$\begin{cases}{\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{2}} }=...=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta_{\mathrm{n}} }}\\{\mathrm{sin}\theta_{\mathrm{1}} +\mathrm{sin}\theta_{\mathrm{2}} +...+\mathrm{sin}\theta_{\mathrm{n}} =\mathrm{n}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{sin}\theta_{\mathrm{1}} =\mathrm{sin}\theta_{\mathrm{2}} =\:\:\:...\:\:\:\:\:\:\:\:=\mathrm{sin}\theta_{\mathrm{n}} }\\{\mathrm{sin}\theta_{\mathrm{1}} +\mathrm{sin}\theta_{\mathrm{2}} +\:\:\:\:...\:\:\:\:+\mathrm{sin}\theta_{\mathrm{n}} =\mathrm{n}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{sin}\theta_{\mathrm{1}} =\mathrm{sin}\theta_{\mathrm{2}} =\:\:\:\:...\:\:\:\:\:=\mathrm{sin}\theta_{\mathrm{n}} =\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{cos}\theta_{\mathrm{1}} =\mathrm{cos}\theta_{\mathrm{2}} =\:\:\:\:...\:\:\:\:=\mathrm{cos}\theta_{\mathrm{n}} =\mathrm{0} \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{cos}\left(\theta_{\mathrm{k}} \right)=\mathrm{0}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right)\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com