Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 5897 by sanusihammed last updated on 04/Jun/16

If four people all said HELLO to each other once. how many times would the word HELLO be spoken ?

$${If}\:{four}\:{people}\:{all}\:{said}\:\:{HELLO}\:{to}\:{each}\:{other}\:{once}.\:{how}\:{many}\: \\ $$$${times}\:{would}\:{the}\:{word}\:\:{HELLO}\:\:{be}\:{spoken}\:? \\ $$

Answered by FilupSmith last updated on 04/Jun/16

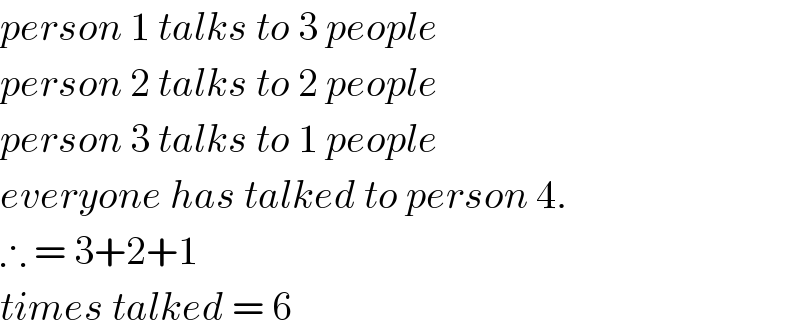
person 1 talks to 3 people person 2 talks to 2 people person 3 talks to 1 people everyone has talked to person 4. ∴ = 3+2+1 times talked = 6

$${person}\:\mathrm{1}\:{talks}\:{to}\:\mathrm{3}\:{people} \\ $$$${person}\:\mathrm{2}\:{talks}\:{to}\:\mathrm{2}\:{people} \\ $$$${person}\:\mathrm{3}\:{talks}\:{to}\:\mathrm{1}\:{people} \\ $$$${everyone}\:{has}\:{talked}\:{to}\:{person}\:\mathrm{4}. \\ $$$$\therefore\:=\:\mathrm{3}+\mathrm{2}+\mathrm{1} \\ $$$${times}\:{talked}\:=\:\mathrm{6} \\ $$

Commented by FilupSmith last updated on 04/Jun/16

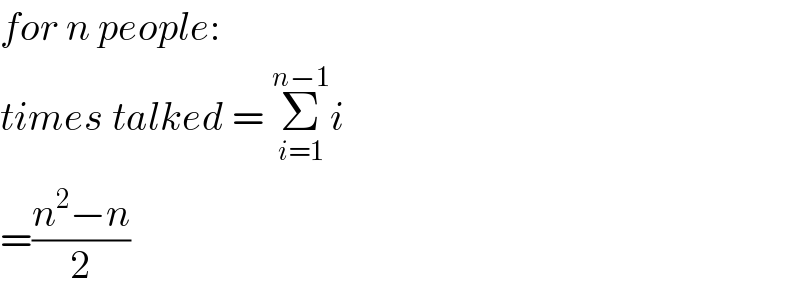
for n people: times talked = Σ_(i=1) ^(n−1) i =((n^2 −n)/2)

$${for}\:{n}\:{people}: \\ $$$${times}\:{talked}\:=\:\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{i} \\ $$$$=\frac{{n}^{\mathrm{2}} −{n}}{\mathrm{2}} \\ $$

Commented by prakash jain last updated on 04/Jun/16

I think if two person say hello both of them will need to speak. so word hello will be spoken 6×2=12 times

$$\mathrm{I}\:\mathrm{think}\:\mathrm{if}\:\mathrm{two}\:\mathrm{person}\:\mathrm{say}\:\mathrm{hello}\:\mathrm{both}\:\mathrm{of}\:\mathrm{them} \\ $$$$\mathrm{will}\:\mathrm{need}\:\mathrm{to}\:\mathrm{speak}. \\ $$$$\mathrm{so}\:\mathrm{word}\:\mathrm{hello}\:\mathrm{will}\:\mathrm{be}\:\mathrm{spoken}\:\mathrm{6}×\mathrm{2}=\mathrm{12}\:\mathrm{times} \\ $$

Commented by FilupSmith last updated on 05/Jun/16

if everyone said hello to each other, but no two people say hello to each other more than once: (1) says hello to 2 3 and 4 (2) says hello to 3 and 4 (1 already seid hello) 3 says hello to 4 everyones talked to 4 so 4 does nothing =3+2+1=6 this is true only if they talk to each other once only.

$${if}\:{everyone}\:{said}\:{hello}\:{to}\:{each}\:{other}, \\ $$$${but}\:{no}\:{two}\:{people}\:{say}\:{hello}\:{to}\:{each}\:{other} \\ $$$${more}\:{than}\:{once}: \\ $$$$\left(\mathrm{1}\right)\:{says}\:{hello}\:{to}\:\mathrm{2}\:\mathrm{3}\:{and}\:\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:{says}\:{hello}\:{to}\:\mathrm{3}\:{and}\:\mathrm{4}\:\left(\mathrm{1}\:{already}\:{seid}\:{hello}\right) \\ $$$$\mathrm{3}\:\mathrm{says}\:\mathrm{hello}\:\mathrm{to}\:\mathrm{4} \\ $$$$\mathrm{everyones}\:\mathrm{talked}\:\mathrm{to}\:\mathrm{4}\:\mathrm{so}\:\mathrm{4}\:\mathrm{does}\:\mathrm{nothing} \\ $$$$=\mathrm{3}+\mathrm{2}+\mathrm{1}=\mathrm{6} \\ $$$$ \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{true}\:\mathrm{only}\:\mathrm{if}\:\mathrm{they}\:\mathrm{talk}\:\mathrm{to}\:\mathrm{each}\:\mathrm{other} \\ $$$$\mathrm{once}\:\mathrm{only}. \\ $$

Commented by FilupSmith last updated on 05/Jun/16

if 4 people said hello to each other without restriction, each person says hello (n−1) times for n people =n(n−1) =4(3) =12

$${if}\:\mathrm{4}\:{people}\:{said}\:{hello}\:{to}\:{each}\:{other} \\ $$$${without}\:{restriction},\:{each}\:{person} \\ $$$${says}\:{hello}\:\left({n}−\mathrm{1}\right)\:{times}\:{for}\:{n}\:{people} \\ $$$$={n}\left({n}−\mathrm{1}\right) \\ $$$$=\mathrm{4}\left(\mathrm{3}\right) \\ $$$$=\mathrm{12} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com