Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 128425 by bramlexs22 last updated on 07/Jan/21

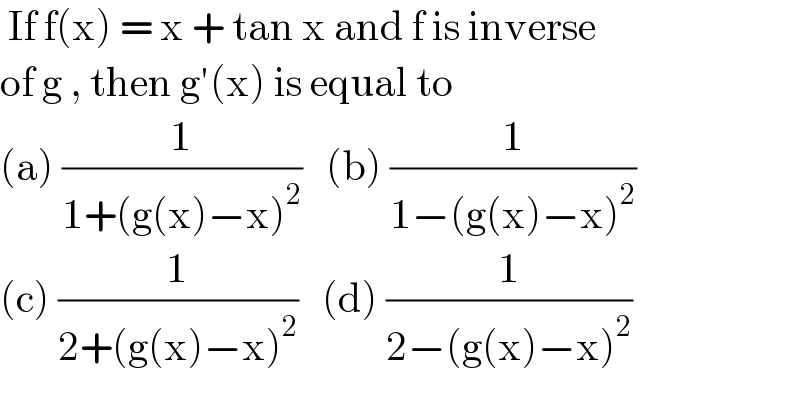
If f(x) = x + tan x and f is inverse of g , then g′(x) is equal to (a) (1/(1+(g(x)−x)^2 )) (b) (1/(1−(g(x)−x)^2 )) (c) (1/(2+(g(x)−x)^2 )) (d) (1/(2−(g(x)−x)^2 ))

$$\:\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\:\mathrm{and}\:\mathrm{f}\:\mathrm{is}\:\mathrm{inverse} \\ $$$$\mathrm{of}\:\mathrm{g}\:,\:\mathrm{then}\:\mathrm{g}'\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left(\mathrm{a}\right)\:\frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} }\:\:\:\left(\mathrm{b}\right)\:\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{c}\right)\:\frac{\mathrm{1}}{\mathrm{2}+\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} }\:\:\:\left(\mathrm{d}\right)\:\frac{\mathrm{1}}{\mathrm{2}−\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} } \\ $$

Answered by liberty last updated on 07/Jan/21

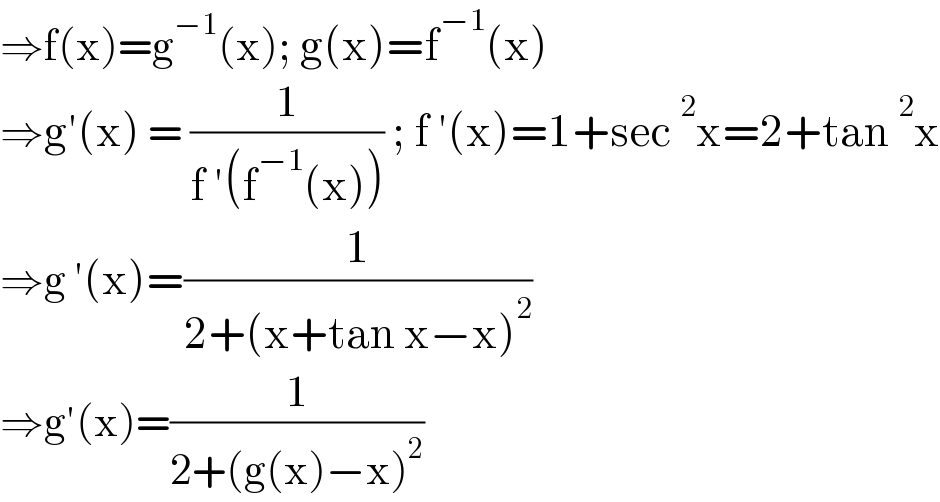
⇒f(x)=g^(−1) (x); g(x)=f^(−1) (x) ⇒g′(x) = (1/(f ′(f^(−1) (x)))) ; f ′(x)=1+sec^2 x=2+tan^2 x ⇒g ′(x)=(1/(2+(x+tan x−x)^2 )) ⇒g′(x)=(1/(2+(g(x)−x)^2 ))

$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right);\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{g}'\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{f}\:'\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)}\:;\:\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}=\mathrm{2}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\mathrm{g}\:'\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}+\left(\mathrm{x}+\mathrm{tan}\:\mathrm{x}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{g}'\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}+\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com