
Previous in Relation and Functions Next in Relation and Functions
Question Number 38367 by Zuarkton last updated on 24/Jun/18
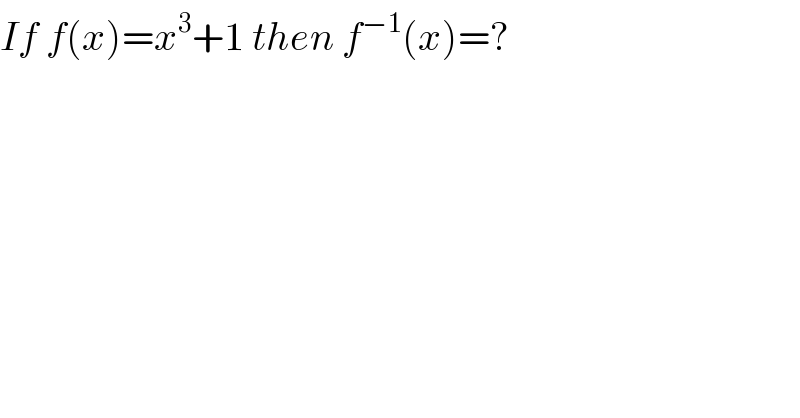
$${If}\:{f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{1}\:{then}\:{f}^{−\mathrm{1}} \left({x}\right)=? \\ $$
Commented by rahul 19 last updated on 24/Jun/18

$$\left({x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$
Commented by Zuarkton last updated on 24/Jun/18

$${Solution}? \\ $$
Answered by MrW3 last updated on 24/Jun/18

$${y}={f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{1} \\ $$$$\Rightarrow{x}=\:^{\mathrm{3}} \sqrt{{y}−\mathrm{1}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\:^{\mathrm{3}} \sqrt{{x}−\mathrm{1}} \\ $$
Answered by Rio Mike last updated on 25/Jun/18
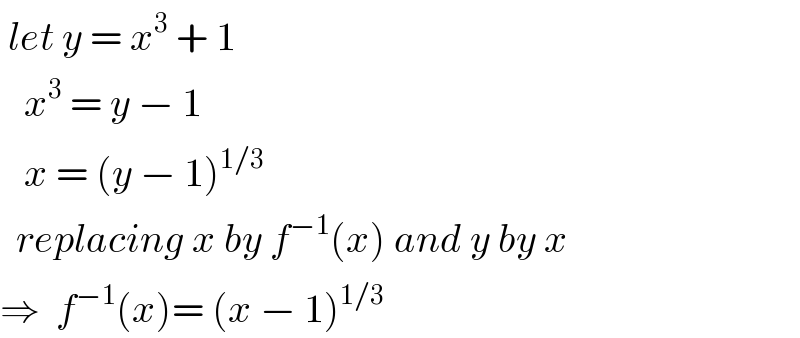
$$\:{let}\:{y}\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{1}\: \\ $$$$\:\:\:{x}^{\mathrm{3}} \:=\:{y}\:−\:\mathrm{1} \\ $$$$\:\:\:{x}\:=\:\left({y}\:−\:\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:{replacing}\:{x}\:{by}\:{f}^{−\mathrm{1}} \left({x}\right)\:{and}\:{y}\:{by}\:{x} \\ $$$$\Rightarrow\:\:{f}^{−\mathrm{1}} \left({x}\right)=\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} \\ $$
