
Question Number 18232 by Joel577 last updated on 17/Jul/17
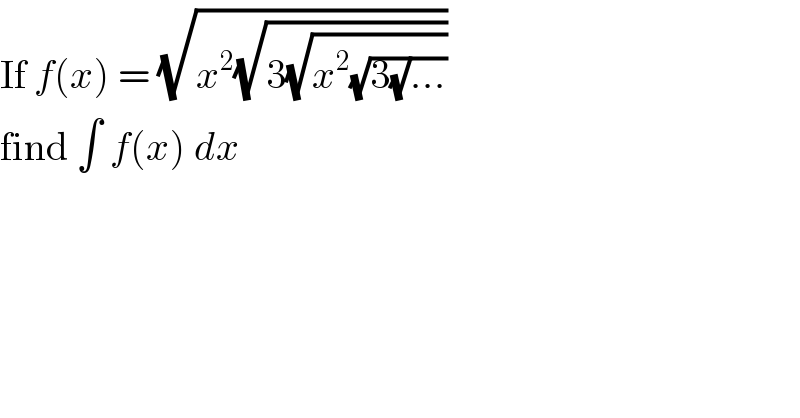
$$\mathrm{If}\:{f}\left({x}\right)\:=\:\sqrt{{x}^{\mathrm{2}} \sqrt{\mathrm{3}\sqrt{{x}^{\mathrm{2}} \sqrt{\mathrm{3}\sqrt{}...}}}} \\ $$$$\mathrm{find}\:\int\:{f}\left({x}\right)\:{dx} \\ $$
Answered by alex041103 last updated on 17/Jul/17
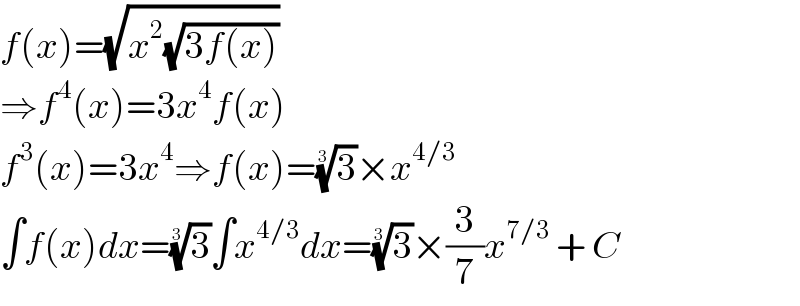
$${f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} \sqrt{\mathrm{3}{f}\left({x}\right)}} \\ $$$$\Rightarrow{f}^{\mathrm{4}} \left({x}\right)=\mathrm{3}{x}^{\mathrm{4}} {f}\left({x}\right) \\ $$$${f}^{\mathrm{3}} \left({x}\right)=\mathrm{3}{x}^{\mathrm{4}} \Rightarrow{f}\left({x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{3}}×{x}^{\mathrm{4}/\mathrm{3}} \\ $$$$\int{f}\left({x}\right){dx}=\sqrt[{\mathrm{3}}]{\mathrm{3}}\int{x}^{\mathrm{4}/\mathrm{3}} {dx}=\sqrt[{\mathrm{3}}]{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{7}}{x}^{\mathrm{7}/\mathrm{3}} \:+\:{C} \\ $$
Commented by Joel577 last updated on 17/Jul/17
$${thank}\:{you}\:{very}\:{much} \\ $$
