Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 187695 by mnjuly1970 last updated on 20/Feb/23

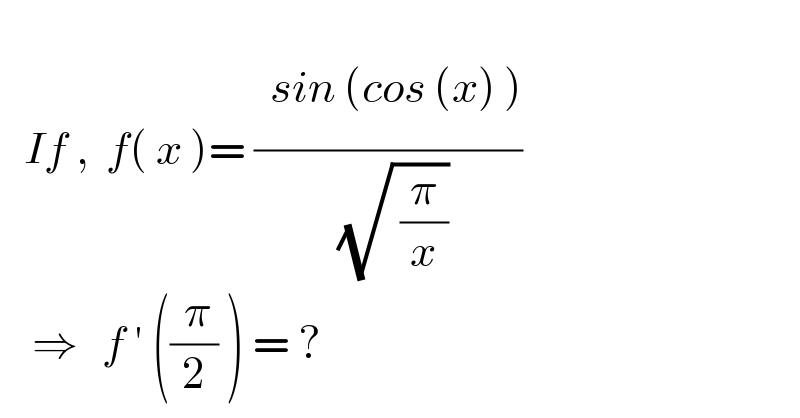
If , f( x )= (( sin_ (cos (x) ))/( ^ (√( (π/x))))) ⇒ f ′ ((( π)/2) ) = ?

$$ \\ $$$$\:\:\:{If}\:,\:\:{f}\left(\:{x}\:\right)=\:\frac{\:\:{si}\underset{} {{n}}\:\left({cos}\:\left({x}\right)\:\right)}{\overset{} {\:}\sqrt{\:\frac{\pi}{{x}}}} \\ $$$$\:\:\:\:\Rightarrow\:\:\:{f}\:'\:\left(\frac{\:\pi}{\mathrm{2}}\:\right)\:=\:? \\ $$

Answered by horsebrand11 last updated on 20/Feb/23

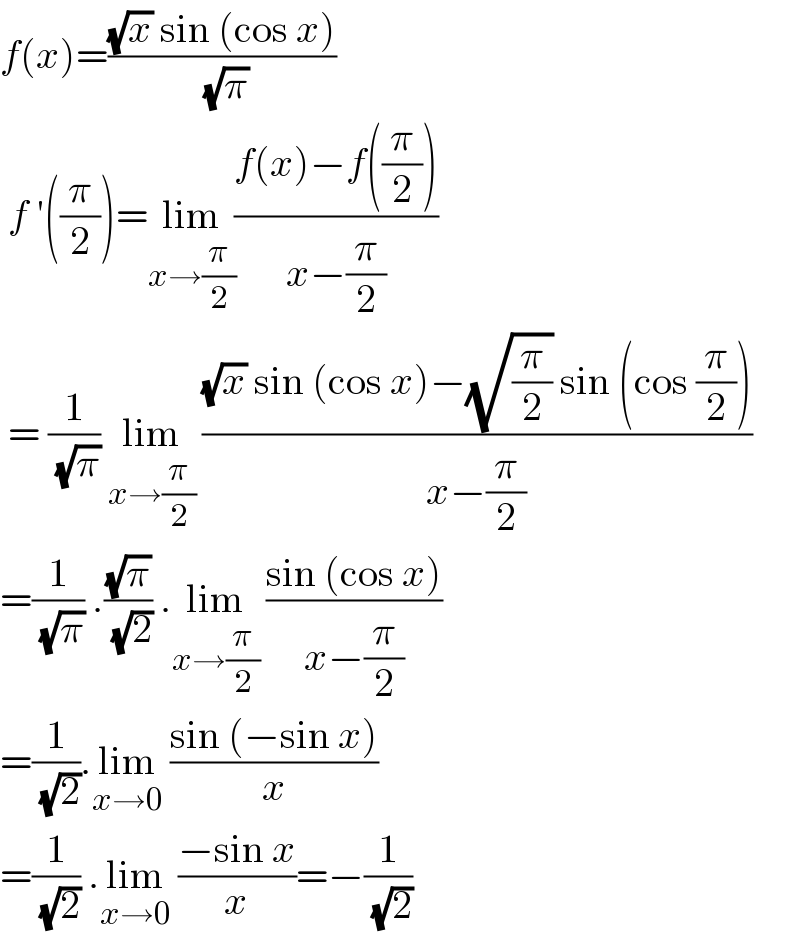
f(x)=(((√x) sin (cos x))/( (√π))) f ′((π/2))=lim_(x→(π/2)) ((f(x)−f((π/2)))/(x−(π/2))) = (1/( (√π))) lim_(x→(π/2)) (((√x) sin (cos x)−(√(π/2)) sin (cos (π/2)))/(x−(π/2))) =(1/( (√π))) .((√π)/( (√2))) .lim_(x→(π/2)) ((sin (cos x))/(x−(π/2))) =(1/( (√2))).lim_(x→0) ((sin (−sin x))/x) =(1/( (√2))) .lim_(x→0) ((−sin x)/x)=−(1/( (√2)))

$${f}\left({x}\right)=\frac{\sqrt{{x}}\:\mathrm{sin}\:\left(\mathrm{cos}\:{x}\right)}{\:\sqrt{\pi}}\: \\ $$$$\:{f}\:'\left(\frac{\pi}{\mathrm{2}}\right)=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left(\frac{\pi}{\mathrm{2}}\right)}{{x}−\frac{\pi}{\mathrm{2}}} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\pi}}\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\sqrt{{x}}\:\mathrm{sin}\:\left(\mathrm{cos}\:{x}\right)−\sqrt{\frac{\pi}{\mathrm{2}}}\:\mathrm{sin}\:\left(\mathrm{cos}\:\frac{\pi}{\mathrm{2}}\right)}{{x}−\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\:.\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\:.\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{cos}\:{x}\right)}{{x}−\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(−\mathrm{sin}\:{x}\right)}{{x}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:{x}}{{x}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$

Answered by cortano12 last updated on 20/Feb/23

f(x)=(((√x) sin (cos x))/( (√π))) f ′(x)=(1/( (√π))) [((sin (cos x))/(2(√x))) −(√x) sin x cos (cos x)] f ′((π/2))=(1/( (√π))) [0−((√π)/( (√2))) .1 ] =−((√2)/2)

$${f}\left({x}\right)=\frac{\sqrt{{x}}\:\mathrm{sin}\:\left(\mathrm{cos}\:{x}\right)}{\:\sqrt{\pi}} \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\pi}}\:\left[\frac{\mathrm{sin}\:\left(\mathrm{cos}\:{x}\right)}{\mathrm{2}\sqrt{{x}}}\:−\sqrt{{x}}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:\left(\mathrm{cos}\:{x}\right)\right] \\ $$$${f}\:'\left(\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\:\sqrt{\pi}}\:\left[\mathrm{0}−\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\:.\mathrm{1}\:\right]\:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com