
Question Number 84861 by Jakir Sarif Mondal last updated on 16/Mar/20
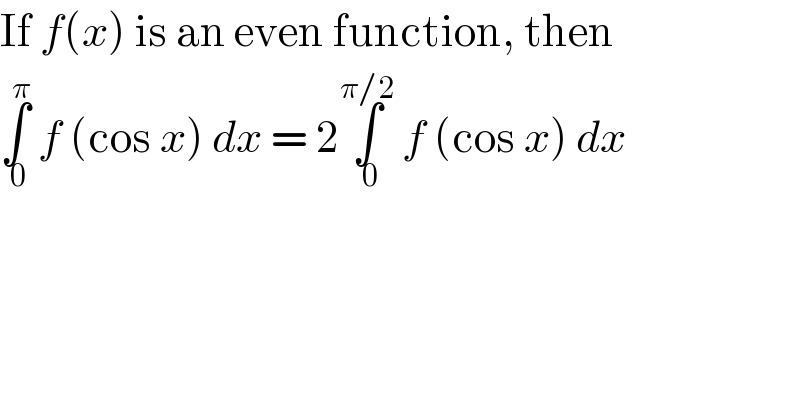
$$\mathrm{If}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{function},\:\mathrm{then} \\ $$$$\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:{f}\:\left(\mathrm{cos}\:{x}\right)\:{dx}\:=\:\mathrm{2}\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:{f}\:\left(\mathrm{cos}\:{x}\right)\:{dx} \\ $$
Commented by mr W last updated on 17/Mar/20
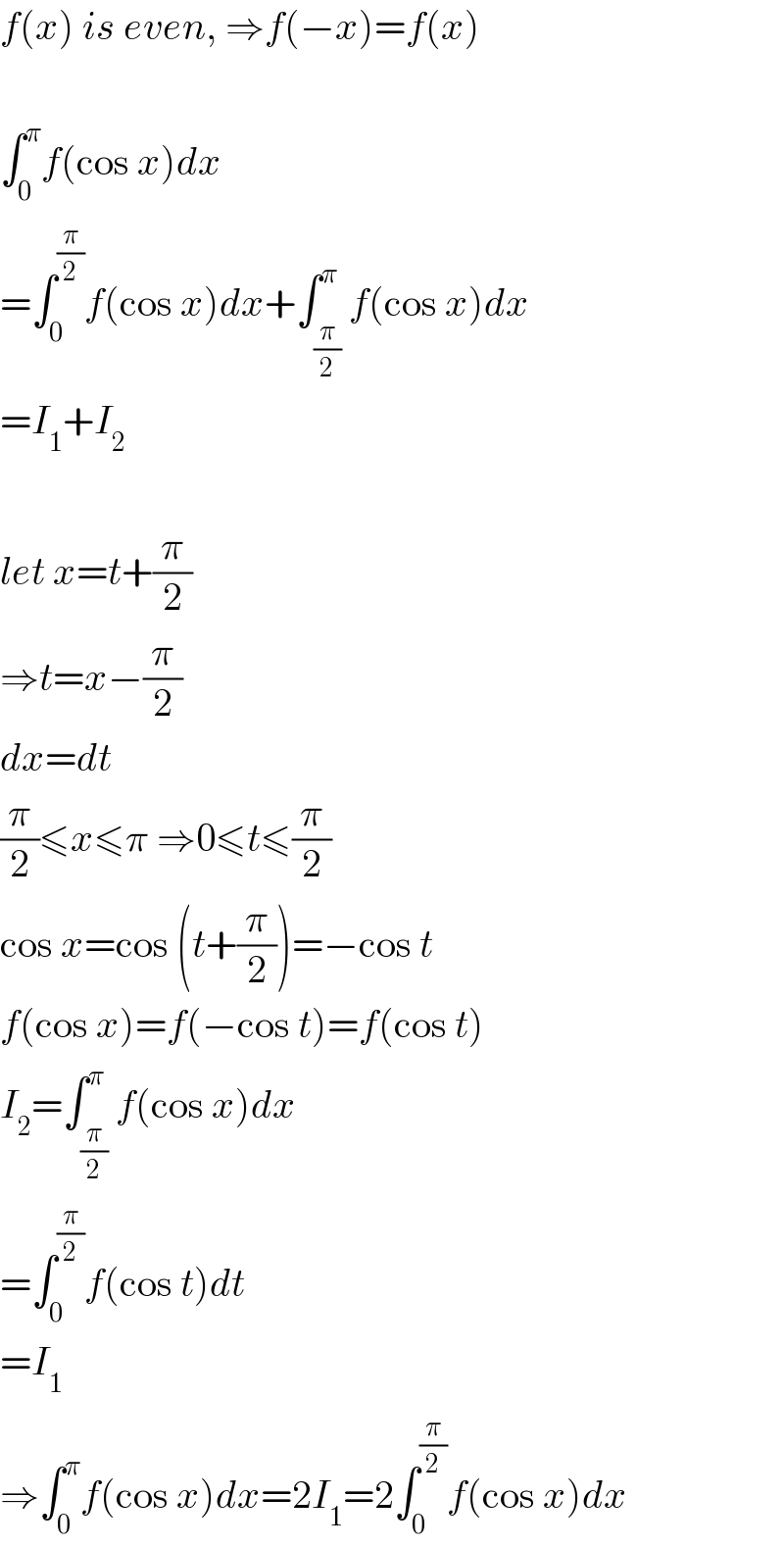
$${f}\left({x}\right)\:{is}\:{even},\:\Rightarrow{f}\left(−{x}\right)={f}\left({x}\right) \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\pi} {f}\left(\mathrm{cos}\:{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left(\mathrm{cos}\:{x}\right){dx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} {f}\left(\mathrm{cos}\:{x}\right){dx} \\ $$$$={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$$ \\ $$$${let}\:{x}={t}+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{t}={x}−\frac{\pi}{\mathrm{2}} \\ $$$${dx}={dt} \\ $$$$\frac{\pi}{\mathrm{2}}\leqslant{x}\leqslant\pi\:\Rightarrow\mathrm{0}\leqslant{t}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{x}=\mathrm{cos}\:\left({t}+\frac{\pi}{\mathrm{2}}\right)=−\mathrm{cos}\:{t} \\ $$$${f}\left(\mathrm{cos}\:{x}\right)={f}\left(−\mathrm{cos}\:{t}\right)={f}\left(\mathrm{cos}\:{t}\right) \\ $$$${I}_{\mathrm{2}} =\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} {f}\left(\mathrm{cos}\:{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left(\mathrm{cos}\:{t}\right){dt} \\ $$$$={I}_{\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} {f}\left(\mathrm{cos}\:{x}\right){dx}=\mathrm{2}{I}_{\mathrm{1}} =\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left(\mathrm{cos}\:{x}\right){dx} \\ $$
