Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 111535 by Aina Samuel Temidayo last updated on 04/Sep/20

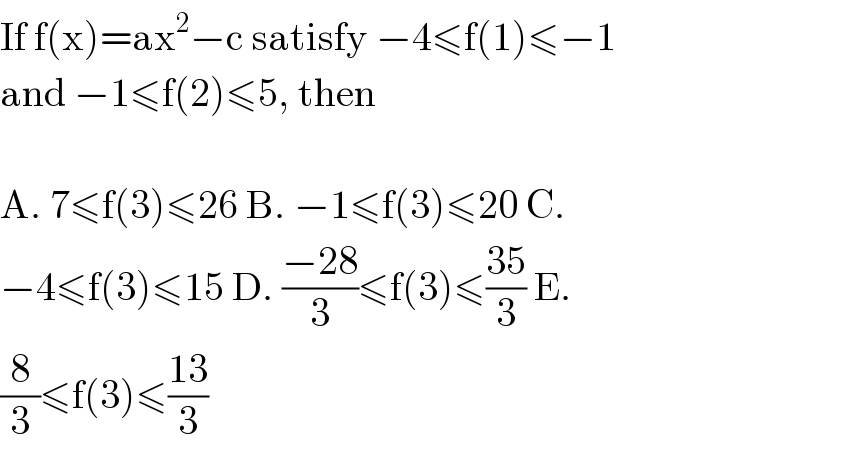
If f(x)=ax^2 −c satisfy −4≤f(1)≤−1 and −1≤f(2)≤5, then A. 7≤f(3)≤26 B. −1≤f(3)≤20 C. −4≤f(3)≤15 D. ((−28)/3)≤f(3)≤((35)/3) E. (8/3)≤f(3)≤((13)/3)

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} −\mathrm{c}\:\mathrm{satisfy}\:−\mathrm{4}\leqslant\mathrm{f}\left(\mathrm{1}\right)\leqslant−\mathrm{1} \\ $$$$\mathrm{and}\:−\mathrm{1}\leqslant\mathrm{f}\left(\mathrm{2}\right)\leqslant\mathrm{5},\:\mathrm{then} \\ $$$$ \\ $$$$\mathrm{A}.\:\mathrm{7}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\mathrm{26}\:\mathrm{B}.\:−\mathrm{1}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\mathrm{20}\:\mathrm{C}. \\ $$$$−\mathrm{4}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\mathrm{15}\:\mathrm{D}.\:\frac{−\mathrm{28}}{\mathrm{3}}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\frac{\mathrm{35}}{\mathrm{3}}\:\mathrm{E}. \\ $$$$\frac{\mathrm{8}}{\mathrm{3}}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\frac{\mathrm{13}}{\mathrm{3}} \\ $$

Answered by 1549442205PVT last updated on 04/Sep/20

−4≤f(1)≤−1⇔−4≤a−c≤−1(1) −1≤f(2)≤5⇔−1≤4a−c≤5.We have { ((−1≤4a−c≤−1)),((−1≥a−c≥−4)) :} Substracting two inequaliries we get 0≤3a≤3⇔0≤a≤1(2). (1)⇔1≤c−a≤4 (3).Adding up (2) (3) we get 1≤c≤5(5) f(3)=9a−c≤9−1=8 f(3)=9a−c≥0−5=−4 Hence −4≤f(3)≤8⇒Choose C

$$−\mathrm{4}\leqslant\mathrm{f}\left(\mathrm{1}\right)\leqslant−\mathrm{1}\Leftrightarrow−\mathrm{4}\leqslant\mathrm{a}−\mathrm{c}\leqslant−\mathrm{1}\left(\mathrm{1}\right) \\ $$$$−\mathrm{1}\leqslant\mathrm{f}\left(\mathrm{2}\right)\leqslant\mathrm{5}\Leftrightarrow−\mathrm{1}\leqslant\mathrm{4a}−\mathrm{c}\leqslant\mathrm{5}.\mathrm{We}\:\mathrm{have} \\ $$$$\begin{cases}{−\mathrm{1}\leqslant\mathrm{4a}−\mathrm{c}\leqslant−\mathrm{1}}\\{−\mathrm{1}\geqslant\mathrm{a}−\mathrm{c}\geqslant−\mathrm{4}}\end{cases} \\ $$$$\mathrm{Substracting}\:\mathrm{two}\:\mathrm{inequaliries}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{0}\leqslant\mathrm{3a}\leqslant\mathrm{3}\Leftrightarrow\mathrm{0}\leqslant\mathrm{a}\leqslant\mathrm{1}\left(\mathrm{2}\right). \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{1}\leqslant\mathrm{c}−\mathrm{a}\leqslant\mathrm{4}\:\left(\mathrm{3}\right).\mathrm{Adding}\:\mathrm{up}\:\left(\mathrm{2}\right)\:\left(\mathrm{3}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{1}\leqslant\mathrm{c}\leqslant\mathrm{5}\left(\mathrm{5}\right) \\ $$$$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{9a}−\mathrm{c}\leqslant\mathrm{9}−\mathrm{1}=\mathrm{8} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{9a}−\mathrm{c}\geqslant\mathrm{0}−\mathrm{5}=−\mathrm{4} \\ $$$$\mathrm{Hence}\:−\mathrm{4}\leqslant\mathrm{f}\left(\mathrm{3}\right)\leqslant\mathrm{8}\Rightarrow\boldsymbol{\mathrm{Choose}}\:\boldsymbol{\mathrm{C}} \\ $$

Commented by Aina Samuel Temidayo last updated on 04/Sep/20

Thanks.

$$\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com