Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194809 by dimentri last updated on 16/Jul/23

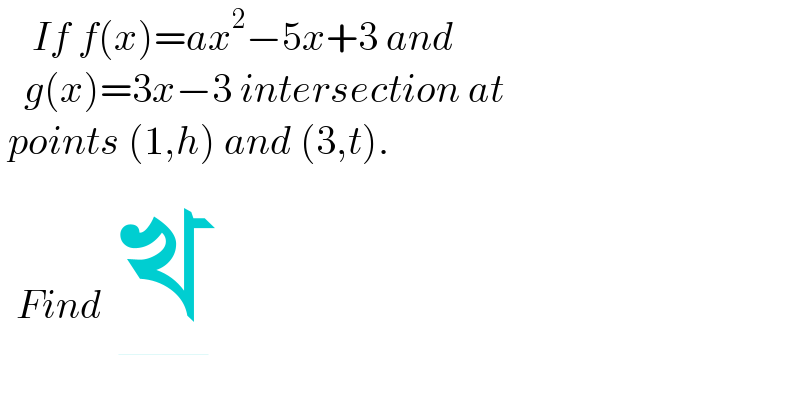
If f(x)=ax^2 −5x+3 and g(x)=3x−3 intersection at points (1,h) and (3,t). Find

$$\:\:\:\:{If}\:{f}\left({x}\right)={ax}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}\:{and}\: \\ $$$$\:\:\:{g}\left({x}\right)=\mathrm{3}{x}−\mathrm{3}\:{intersection}\:{at} \\ $$$$\:{points}\:\left(\mathrm{1},{h}\right)\:{and}\:\left(\mathrm{3},{t}\right). \\ $$$$\:\:{Find}\:\:\underline{ } \\ $$

Answered by horsebrand11 last updated on 16/Jul/23

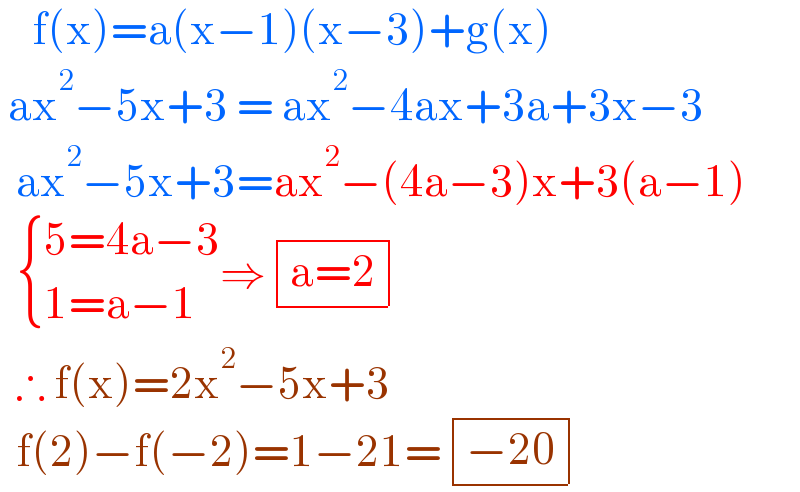
f(x)=a(x−1)(x−3)+g(x) ax^2 −5x+3 = ax^2 −4ax+3a+3x−3 ax^2 −5x+3=ax^2 −(4a−3)x+3(a−1) { ((5=4a−3)),((1=a−1)) :}⇒ determinant (((a=2))) ∴ f(x)=2x^2 −5x+3 f(2)−f(−2)=1−21= determinant (((−20)))

$$\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\:\mathrm{ax}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3}\:=\:\mathrm{ax}^{\mathrm{2}} −\mathrm{4ax}+\mathrm{3a}+\mathrm{3x}−\mathrm{3} \\ $$$$\:\:\mathrm{ax}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3}=\mathrm{ax}^{\mathrm{2}} −\left(\mathrm{4a}−\mathrm{3}\right)\mathrm{x}+\mathrm{3}\left(\mathrm{a}−\mathrm{1}\right) \\ $$$$\:\:\begin{cases}{\mathrm{5}=\mathrm{4a}−\mathrm{3}}\\{\mathrm{1}=\mathrm{a}−\mathrm{1}}\end{cases}\Rightarrow\begin{array}{|c|}{\mathrm{a}=\mathrm{2}}\\\hline\end{array} \\ $$$$\:\:\therefore\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{3} \\ $$$$\:\:\mathrm{f}\left(\mathrm{2}\right)−\mathrm{f}\left(−\mathrm{2}\right)=\mathrm{1}−\mathrm{21}=\begin{array}{|c|}{−\mathrm{20}}\\\hline\end{array} \\ $$

Commented by dimentri last updated on 16/Jul/23

x

$$\:\:\:\:\:\:\underline{\underbrace{\boldsymbol{{x}}}} \\ $$

Answered by Rasheed.Sindhi last updated on 16/Jul/23

f(1)=g(1)=h a(1)^2 −5(1)+3=3(1)−3=h a−2=0 a=2 f(x)=2x^2 −5x+3 f(2)−f(−2) ={2(2)^2 −5(2)+3}−{2(−2)^2 −5(−2)+3} =1−21=−20 •“(3,t) is intersection point”is unnecessary.One common point is sufficient here.

$${f}\left(\mathrm{1}\right)={g}\left(\mathrm{1}\right)={h} \\ $$$${a}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{1}\right)+\mathrm{3}=\mathrm{3}\left(\mathrm{1}\right)−\mathrm{3}={h} \\ $$$${a}−\mathrm{2}=\mathrm{0} \\ $$$${a}=\mathrm{2} \\ $$$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3} \\ $$$${f}\left(\mathrm{2}\right)−{f}\left(−\mathrm{2}\right) \\ $$$$\:\:\:\:=\left\{\mathrm{2}\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}\right)+\mathrm{3}\right\}−\left\{\mathrm{2}\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}\left(−\mathrm{2}\right)+\mathrm{3}\right\} \\ $$$$\:\:\:=\mathrm{1}−\mathrm{21}=−\mathrm{20} \\ $$$$\bullet``\left(\mathrm{3},{t}\right)\:{is}\:{intersection}\:{point}''{is} \\ $$$${unnecessary}.{One}\:{common}\:{point} \\ $$$${is}\:{sufficient}\:{here}. \\ $$

Commented by dimentri last updated on 16/Jul/23

$$\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com